题目内容
在正三棱锥内作一内切球,棱锥的侧面与底面成60°角,球的体积为4
解析:作一条侧棱和高的截面如图所示.
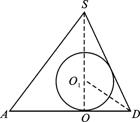
设棱锥的高为h ,底面边长为a,面积为S,球的半径为R,V棱锥=![]() Sh.
Sh.
∵S=![]() a2sin60°=
a2sin60°=![]() a2,
a2,
∴V棱锥=![]() a2h.∵V球=
a2h.∵V球=![]() πR3,
πR3,
∴R3=![]() (而V球=4
(而V球=4![]() π3).
π3).
在△OO1D中,OD=OO1·cot![]() =
=![]()
![]() .
.
在△OSD中,h=OD·tan60°=3![]() =3
=3![]() ,a=2
,a=2![]() ·OD=6
·OD=6![]() ,∴V棱锥=
,∴V棱锥=![]() a2h=
a2h=![]() ·36(
·36(![]() )2·3·(
)2·3·(![]() )=81π2.
)=81π2.
温馨提示
在解答表面积、体积时,首先选定所需图形,作出相应的高.注意垂足的位置的确定.在直角三角形中求解,特别是所给角的确定,充分利用已知条件,把它们转化到平面上去解决.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目