题目内容

已知数列{a_n}满足： $数学公式$
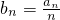（1）设 $数学公式$ ，求数列{b_n}的通项公式；
（2）若对任意给定的正整数m，使得不等式a_n+t≥2m（n∈N^*）成立的所有n中的最小值为m+2，求实数t的取值范围．

解：（1）由 $\text{[math]}$ 得 $\text{[math]}$ ，
即 $\text{[math]}$
∴ $\text{[math]}$
$\text{[math]}$
…
$\text{[math]}$ ，
以上各式相加得 $\text{[math]}$ ， $\text{[math]}$ （n≥2）
又b₁=a₁=1，也适合上式，∴ $\text{[math]}$ ．
（2）由 $\text{[math]}$ ，
则 $\text{[math]}$ ，
据题意，区间 $\text{[math]}$ 内的最小正整数为m+2，
所以 $\text{[math]}$ ，
解得-3≤t＜-1
分析：（1）将 $\text{[math]}$ 变形构造得出 $\text{[math]}$ ，即有 $\text{[math]}$ ，用叠加法能求数列{b_n}的通项公式．
（2）由（1）a_n=2n-1代入所给的不等式，解此关于n的不等式，解集内最小正整数为m+2，再建立相关不等式求t的取值范围．
点评：本题考查数列通项公式、叠加法求通项、不等式恒成立．考查转化构造、分析解决问题、计算、逻辑思维等能力．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知数列{a_n}满足：a₁=1且an+1=

， n∈N*．
（1）若数列{b_n}满足：bn=

(n∈N*)，试证明数列b_n-1是等比数列；
（2）求数列{a_nb_n}的前n项和S_n；
（3）数列{a_n-b_n}是否存在最大项，如果存在求出，若不存在说明理由．

已知数列{a_n}满足

an=2n+1则{a_n}的通项公式

已知数列{a_n}满足：a₁=

（n≥2，n∈N^*）．
（1）求数列{a_n}的通项公式；
（2）证明：对于一切正整数n，不等式a₁•a₂•…a_n＜2•n！

已知数列{a_n}满足a_n+1=|a_n-1|（n∈N^*）
（1）若a1=

，求a_n；
（2）若a₁=a∈（k，k+1），（k∈N^*），求{a_n}的前3k项的和S_3k（用k，a表示）

（2012•北京模拟）已知数列{a_n}满足a_n+1=a_n+2，且a₁=1，那么它的通项公式a_n等于