题目内容
已知P是椭画 +
+ =1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且
=1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且 =2
=2 ,则|
,则| |的值为( )
|的值为( )A.

B.4
C.

D.

【答案】分析:先求出焦点坐标及准线方程,由向量间的关系得出 点Q 分有向线段F1P 成的比为λ=2,由定比分点坐标公式求得 Q的横坐标,代入椭圆的方程可得Q的纵坐标,进而求得|QF1|.
解答: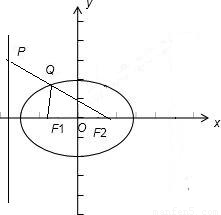 解:如图F1(-3,0)、F2(3,0),左准线l方程x=-
解:如图F1(-3,0)、F2(3,0),左准线l方程x=-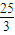 ,
,
∵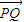 =2
=2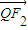 ,∴点 Q 分有向线段PF2成的比为λ=2,
,∴点 Q 分有向线段PF2成的比为λ=2,
设 Q(m,n),则由定比分点坐标公式得
m=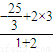 =-
=- ,
,
把Q(m,n)代入椭圆的方程得 n=±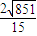 ,
,
∴由两点间的距离公式得|QF1|=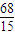 ,
,
故选D.
点评:本题考查椭圆的简单性质、向量运算,以及定比分点坐标公式的应用,体现了数形结合的数学思想.
解答:
 解:如图F1(-3,0)、F2(3,0),左准线l方程x=-
解:如图F1(-3,0)、F2(3,0),左准线l方程x=-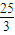 ,
,∵
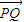 =2
=2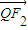 ,∴点 Q 分有向线段PF2成的比为λ=2,
,∴点 Q 分有向线段PF2成的比为λ=2,设 Q(m,n),则由定比分点坐标公式得
m=
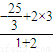 =-
=- ,
,把Q(m,n)代入椭圆的方程得 n=±
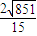 ,
,∴由两点间的距离公式得|QF1|=
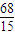 ,
,故选D.
点评:本题考查椭圆的简单性质、向量运算,以及定比分点坐标公式的应用,体现了数形结合的数学思想.

练习册系列答案
相关题目
 +
+ =1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且
=1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且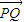 =2
=2 ,则|
,则| |的值为( )
|的值为( )

