题目内容
如图,已知四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD,PA=AD=2,点M、N分别在棱PD、PC上,且PC⊥平面AMN.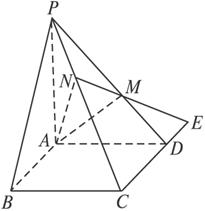
(1)求证:AM⊥PD;
(2)求二面角P-AM-N的大小;
(3)求直线CD与平面AMN所成的角的大小.
解:(1)证明:∵四边形ABCD是正方形,
∴CD⊥AD.又∵PA⊥底面ABCD,
∴PA⊥CD.故CD⊥平面PAD.
又AM?平面PAD,则CD⊥AM,而PC⊥平面AMN,有PC⊥AM,则AM⊥平面PCD,
故AM⊥PD.
(2)∵AM⊥平面PCD(已证),
∴AM⊥PM,AM⊥NM,
故∠PMN为二面角PAMN的平面角,
又∵PN⊥平面AMN,∴PN⊥NM.
在Rt△PCD中,CD=2,PD=2![]() ,则PC=2
,则PC=2![]() ,
,
∵PA=AD,AM⊥PD,
∴M为PD的中点,则PM=![]() PD=
PD=![]() .
.
由Rt△PMN∽Rt△PCD,得MN=![]() ,
,
则cos∠PMN=![]() ,
,
故∠PMN=arccos![]() ,则二面角P-AM-N为arccos
,则二面角P-AM-N为arccos![]() .
.
(3)延长NM、CD交于点E,∵PC⊥平面AMN,
∴NE为CE在平面AMN内的射影.
∴∠CEN为CD(即CE)与平面AMN所成的角.
又CD⊥PD,EN⊥PN,则有∠CEN=∠MPN.
∵sin∠MPN=![]() ,且∠MPN∈(0,
,且∠MPN∈(0,![]() ),
),
∴∠MPN=arcsin![]() .
.
故CD与平面AMN所成的角为arcsin![]() .
.


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,