题目内容
已知| |=2|
|=2| |≠0,且关于x的方程x2+|
|≠0,且关于x的方程x2+| |x+
|x+ ·
· =0有实根,则
=0有实根,则 与
与 的夹角的取值范围是
的夹角的取值范围是
A. | B. | C. | D.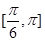 |
B
解析试题分析:因为方程x2+| |x+
|x+ ·
· =0有实根,所以
=0有实根,所以 ,
,
所以 =
= 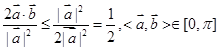 ,所以
,所以 与
与 的夹角的取值范围是
的夹角的取值范围是 ,选B。
,选B。
考点:本题主要考查平面向量的数量积,一元二次方程根的情况。
点评:小综合题,已知中给定了| |=2|
|=2| |≠0,利用方程x2+|
|≠0,利用方程x2+| |x+
|x+ ·
· =0有实根,又可以得到|
=0有实根,又可以得到| |,|
|,| |的另一关系,故
|的另一关系,故 与
与 的夹角的取值范围可求。
的夹角的取值范围可求。

练习册系列答案
相关题目
已知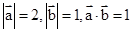 ,,则向量
,,则向量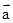 在
在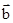 方向上的投影是( )
方向上的投影是( )
A.- | B.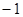 | C. | D.1 |
已知平面向量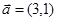 ,
,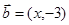 ,且
,且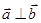 ,则
,则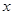 的值为( )
的值为( )
| A.-3 | B.-1 | C.1 | D.3 |
设向量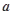 ,
, 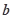 满足:
满足: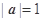 ,
, 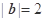 ,
,  , 则
, 则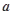 与
与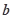 的夹角是( )
的夹角是( )
A.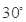 | B.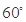 | C. | D.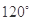 |
O是锐角三角形ABC的外心,由O向边BC,CA,AB引垂线,垂足分别是D,E,F,给出下列命题:
① ;
;
②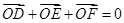 ;
;
③ :
: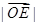 :
: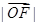 =cosA:cosB:cosC;
=cosA:cosB:cosC;
④ ,使得
,使得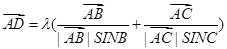 。
。
以上命题正确的个数是( )
| A.1 | B.2 | C.3 | D.4; |
如图:在平行四边形 中,
中, 与
与 交于点
交于点
 ,设
,设
 = ( )
= ( )
A. | B. |
C.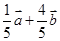 | D. |
不共线的两个向量 ,且
,且 与
与 垂直,
垂直, 垂直,
垂直, 与
与 的夹角的余弦值为( )
的夹角的余弦值为( )
A. | B. | C. | D. |
 、
、 、
、 ,且满足
,且满足 ,|
,|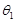 ,
,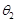 ,
, ,则它们的大小关系是( )
,则它们的大小关系是( )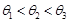


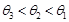
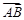 |=a,|
|=a,|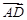 |=b,则
|=b,则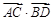 =
=