题目内容
已知等比数列{an}前n项和为Sn,且a1=1,S6=28S3,各项均为正数的等差数列{bn}的前n项和为Tn且T3=15.
(1)求数列{an}的通项公式和b2;
(2)若a1+b1,a2+b2,a3+b3成等比数列,求Tn;
(3)在(2)的条件下证明 .
.
解:(1)由已知得 ∴
∴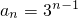
又{bn}为各项均为正数的等差数列,所以T3=3b2=15,∴b2=5
(2)∵a1+b1,a2+b2,a3+b3成等比数列,
设等差数列{bn}的公差为d
∴(3+5)2=(6-d)(14+d)
∴d=2,d=-10(舍去)
∴bn=2n+1,b1=3
∴
(3)由(2)知

= =
=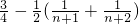

分析:(1)由题意可求q,进而得{an}的通项公式,再由等差数列的性质易得b2的值;
(2)由a1+b1,a2+b2,a3+b3成等比数列,可求数列{bn}的公差,即得数列{bn}的通项为bn=2n+1,可求和;(3)由(2)知 ,符合用裂项相消法求和,即得结论.
,符合用裂项相消法求和,即得结论.
点评:本题为等差等比数列的综合应用,涉及裂项相消法,准确利用公式是解决问题的关键,属中档题.
 ∴
∴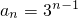
又{bn}为各项均为正数的等差数列,所以T3=3b2=15,∴b2=5
(2)∵a1+b1,a2+b2,a3+b3成等比数列,
设等差数列{bn}的公差为d
∴(3+5)2=(6-d)(14+d)
∴d=2,d=-10(舍去)
∴bn=2n+1,b1=3
∴

(3)由(2)知


=
 =
=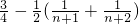

分析:(1)由题意可求q,进而得{an}的通项公式,再由等差数列的性质易得b2的值;
(2)由a1+b1,a2+b2,a3+b3成等比数列,可求数列{bn}的公差,即得数列{bn}的通项为bn=2n+1,可求和;(3)由(2)知
 ,符合用裂项相消法求和,即得结论.
,符合用裂项相消法求和,即得结论.点评:本题为等差等比数列的综合应用,涉及裂项相消法,准确利用公式是解决问题的关键,属中档题.

练习册系列答案
相关题目