题目内容
2.已知函数f(x)=mx-alnx-m,g(x)=$\frac{x}{{e}^{x-1}}$,其中m,a均为实数.(Ⅰ)求函数g(x)的极值;
(Ⅱ)设m=1,a<0,若对任意的x1、x2∈[3,4](x1≠x2),|f(x2)-f(x1)|<|$\frac{1}{g({x}_{2})}$-$\frac{1}{g({x}_{1})}$|恒成立,求实数a的最小值.
分析 (Ⅰ)对函数g(x)求导,得到g'(x)=0,得到极值点,求出极值.
(Ⅱ)不妨设x2>x1,则$|f({x_2})-f({x_1})|<|{\frac{1}{{g({x_2})}}-\frac{1}{{g({x_1})}}}|$等价于:f(x2)-f(x1)<h(x2)-h(x1),即f(x2)-h(x2)<f(x1)-h(x1),分离参数,利用导数求最值求出参数范围即可.
解答 解:(Ⅰ)$g'(x)=\frac{1-x}{{{e^{x-1}}}}$,令g'(x)=0,得x=1,列表如下:
| x | (-∞,1) | 1 | (1,+∞) |
| g'(x) | + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
(Ⅱ)当m=1时,a<0时,f(x)=x-alnx-1,x∈(0,+∞),
∵$f'(x)=\frac{x-a}{x}>0$在[3,4]恒成立,∴f(x)在[3,4]上为增函数,
设$h(x)=\frac{1}{g(x)}=\frac{{{e^{x-1}}}}{x}$,∵$h'(x)=\frac{{{e^{x-1}}(x-1)}}{x^2}>0$在[3,4]上恒成立,
∴h(x)在[3,4]上为增函数,
不妨设x2>x1,则$|f({x_2})-f({x_1})|<|{\frac{1}{{g({x_2})}}-\frac{1}{{g({x_1})}}}|$等价于:f(x2)-f(x1)<h(x2)-h(x1),即f(x2)-h(x2)<f(x1)-h(x1),
设u(x)=f(x)-h(x)=$x-alnx-1-\frac{{{e^{x-1}}}}{x}$,则u(x)在[3,4]上为减函数,
∴$u'(x)=1-\frac{a}{x}-\frac{{{e^{x-1}}(x-1)}}{x^2}≤0$在[3,4]上恒成立,
∴$a≥x-{e^{x-1}}+\frac{{{e^{x-1}}}}{x}$恒成立,∴$a≥{(x-{e^{x-1}}+\frac{{{e^{x-1}}}}{x})_{max}}$,x∈[3,4],
设$v(x)=x-{e^{x-1}}+\frac{{{e^{x-1}}}}{x}$,∵$v'(x)=1-{e^{x-1}}+\frac{{{e^{x-1}}(x-1)}}{x^2}=1-{e^{x-1}}[{(\frac{1}{x}-\frac{1}{2})^2}+\frac{3}{4}]$,x∈[3,4],
∴${e^{x-1}}[{(\frac{1}{x}-\frac{1}{2})^2}+\frac{3}{4}]>\frac{3}{4}{e^2}>1$,∴v'(x)<0,v(x)为减函数,
∴v(x)在[3,4]上的最大值$v(3)=3-\frac{2}{3}{e^2}$,∴$a≥3-\frac{2}{3}{e^2}$,∴a的最小值为$3-\frac{2}{3}{e^2}$;
点评 本题主要考查了利用导数求函数极值和利用导数求参数范围,属于中档题型,在高考中经常涉及.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如图所示的程序框图运行结束后,输出的集合中包含的元素个数为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
10.已知抛物线x2=-4$\sqrt{5}$y的焦点与双曲线$\frac{x^2}{a}+\frac{y^2}{4}$=1(a∈R)的一焦点重合,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
17.已知集合A={x|y=lg(x-3)},B={x|x≤5},则A∪B=( )
| A. | {x|3<x≤5} | B. | {x|x≥5} | C. | {x|x<3} | D. | R |
7.直线l:8x-6y-3=0被圆O:x2+y2-2x+a=0所截得弦的长度为$\sqrt{3}$,则实数a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1-$\frac{{\sqrt{13}}}{2}$ |
11.已知直线y=ax+1经过抛物线y2=4x的焦点,则该直线的倾斜角为( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
12.已知球的半径为4,则这个球的表面积是( )
| A. | 32π | B. | 40π | C. | 64π | D. | 72π |
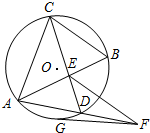 如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.
如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.