题目内容
已知正三角形 的边长为
的边长为 ,点
,点 分别是边
分别是边 上的动点,且满足点
上的动点,且满足点 关于直线
关于直线 的对称点在边
的对称点在边 上,则
上,则 的最小值为 .
的最小值为 .

解析试题分析:设点 关于直线
关于直线 的对称点为
的对称点为 ,
, B=x,由对称性
B=x,由对称性
设 D=AD=t,则BD=2-t,在ΔB
D=AD=t,则BD=2-t,在ΔB D中应用余弦定理,得,
D中应用余弦定理,得,
t²=(2-t)²+x²-2(2-t)xcos60°
化简得,t= ,
,
当且仅当 时,
时, 的最小值为
的最小值为 。
。
考点:余弦定理的应用,均值定理的应用。
点评:中档题,本题综合性较强,首先需要利用对称性,确定三角形中的边长关系,利用余弦定理确定函数式,应用均值定理求解。应用均值定理,要注意“一正,二定,三相等”,缺一不可。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
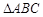 中,若
中,若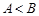 ,则
,则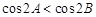 ;
;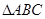 的三个内角,则
的三个内角,则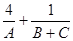 的最小值为
的最小值为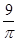
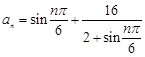
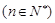 ,则数列
,则数列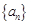 中的最小项为
中的最小项为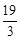 ;
;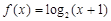 ,且
,且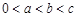 ,则
,则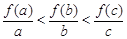 ;
;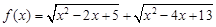 的最小值为
的最小值为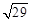 .
.  中,若
中,若 ,则
,则 的大小为 。
的大小为 。 ,点D在BC边上,∠ADC=
,点D在BC边上,∠ADC= ,则AD的长为
,则AD的长为 
 中,
中, , 则
, 则 的值为 .
的值为 . ,那么BC= ;
,那么BC= ; 中,角
中,角 ,
,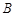 ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,设
,设 为△
为△ ,则
,则 是锐角
是锐角 的外接圆的圆心,且
的外接圆的圆心,且 ,其外接圆半径为
,其外接圆半径为 ,若
,若 ,则
,则 ____
____ 

 的对边分别为
的对边分别为 ,
, 则
则 .
.