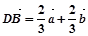题目内容
下列命题中
①“若ab=0,则a=0或b=0”的逆命题;
②“若x2+y2≠0,则x,y不全为零”的否命题;
③“?x∈R,使x2+1>3x”的否定;
④“若m>0,则x2+x-m=0有实根”的逆否命题.
其中正确的是
①“若ab=0,则a=0或b=0”的逆命题;
②“若x2+y2≠0,则x,y不全为零”的否命题;
③“?x∈R,使x2+1>3x”的否定;
④“若m>0,则x2+x-m=0有实根”的逆否命题.
其中正确的是
①②④
①②④
.分析:①写出命题的逆命题,然后判断.②先写出否命题,然后判断.③根据含有量词的命题否定的规律,得到③错误.④判断原命题即可.
解答:解:①“若ab=0,则a=0或b=0”的逆命题是:“若a=0或b=0,则ab=0”,所以①正确.
②原命题的否命题为:“若x2+y2=0,则x,y全为零,”,所以②正确.
③“?x∈R,使x2+1>3x”的否定是:“?x∈R,使x2+1≤3x”.
当x=0时,x2+1=1>0=3x,故“?x∈R,使x2+1≤3x”为假命题.所以③错误.
④由于m>0,则△=12-4(-m)=1+4m>0
故“若m>0,则x2+x-m=0有实根”为真命题,
所以原命题的逆否命题正确,所以④正确.
故答案为:①②④
②原命题的否命题为:“若x2+y2=0,则x,y全为零,”,所以②正确.
③“?x∈R,使x2+1>3x”的否定是:“?x∈R,使x2+1≤3x”.
当x=0时,x2+1=1>0=3x,故“?x∈R,使x2+1≤3x”为假命题.所以③错误.
④由于m>0,则△=12-4(-m)=1+4m>0
故“若m>0,则x2+x-m=0有实根”为真命题,
所以原命题的逆否命题正确,所以④正确.
故答案为:①②④
点评:本题以命题真假的判断为载体,着重考查了四种命题及其相互关系和含有量词的命题的否定等知识点,属于基础题.

练习册系列答案
相关题目
 平面M,直线b
平面M,直线b 平面M,且a
平面M,且a b=φ,则a//平面M;
b=φ,则a//平面M;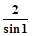 ;
;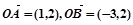 , O为坐标原点,则
, O为坐标原点,则 在
在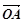 方向上的投影是
方向上的投影是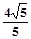 ;
;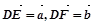 ,则
,则