题目内容
某人玩硬币走跳棋的游戏,已知硬币出现正、反面的概率都是
.棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.
(Ⅰ)求:P0,Pl,P2;
(Ⅱ)求证:Pn-Pn-1=-
(Pn-1-Pn-2);(n≤99,n∈N)
(Ⅲ)求:玩该游戏获胜的概率.
| 1 |
| 2 |
(Ⅰ)求:P0,Pl,P2;
(Ⅱ)求证:Pn-Pn-1=-
| 1 |
| 2 |
(Ⅲ)求:玩该游戏获胜的概率.
分析:(I)棋子在0站是一个必然事件,得到发生的概率等于1,掷出朝上的点数为1或2,棋子向前跳一站;若掷出其余点数,则棋子向前跳两站,根据正方体各个面出现的概率得到结果.
(II)由题意知连续三项之间的关系,根据得到的关系式,仿写一个关系式,两个式子相减,构造一个新数列是连续两项之比是一个常数,得到等比数列.
(III)写出所有的式子,把所有的式子相加,利用累加的方法消去中间项得到首项和末项之间的关系,得到玩该游戏获胜的概率.
(II)由题意知连续三项之间的关系,根据得到的关系式,仿写一个关系式,两个式子相减,构造一个新数列是连续两项之比是一个常数,得到等比数列.
(III)写出所有的式子,把所有的式子相加,利用累加的方法消去中间项得到首项和末项之间的关系,得到玩该游戏获胜的概率.
解答:解:(Ⅰ)依题意,得 P0=1,P1=
,P2=
+
×
=
(Ⅱ) 依题意,棋子跳到第n站(2≤n≤99)有两种可能:
第一种,棋子先到第n-2站,又掷出反面,其概率为
Pn-2;
第二种,棋子先到第n-1站,又掷出正面,其概率为
Pn-1;
∴Pn=
+
∴Pn-Pn-1=
Pn-1+
Pn-2-Pn-1=-
Pn-1+
Pn-2
即Pn-Pn-1=-(
Pn-1-
Pn-2)(2≤n≤99)
(Ⅲ) 由(II)可知,数列{Pn-Pn-1}(1≤n≤99)是首项为P1-P0=-
,
公比为
的等比数列,
于是,有P99=P0+(P1-P0)+(P2-P1)+(P3-P2)+…+(P99-P98)=1+(-
)+(-
)2+(-
)3+…+(-
)99=
[1-(
)100]
因此,玩该游戏获胜的概率为
[1-(
)100].
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
(Ⅱ) 依题意,棋子跳到第n站(2≤n≤99)有两种可能:
第一种,棋子先到第n-2站,又掷出反面,其概率为
| 1 |
| 2 |
第二种,棋子先到第n-1站,又掷出正面,其概率为
| 1 |
| 2 |
∴Pn=
| 1 |
| 2 |
| P | n-1 |
| 1 |
| 2 |
| P | n-2 |
∴Pn-Pn-1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即Pn-Pn-1=-(
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ) 由(II)可知,数列{Pn-Pn-1}(1≤n≤99)是首项为P1-P0=-
| 1 |
| 2 |
公比为
| 1 |
| 2 |
于是,有P99=P0+(P1-P0)+(P2-P1)+(P3-P2)+…+(P99-P98)=1+(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
因此,玩该游戏获胜的概率为
| 2 |
| 3 |
| 1 |
| 2 |
点评:本题考查概率的实际应用,是一个中档题目,题目涉及到概率的计算,本题解题的关键是看出题目中要利用累加的方法.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 .棋盘上标有第0站、第1站、第2站、…、第m(m∈N,m≥100)站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第m-1站(胜利大本营)或第m站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.
.棋盘上标有第0站、第1站、第2站、…、第m(m∈N,m≥100)站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第m-1站(胜利大本营)或第m站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn. .
. .棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.
.棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn. ;(n≤99,n∈N)
;(n≤99,n∈N) .棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.
.棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.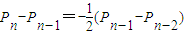 ;(n≤99,n∈N)
;(n≤99,n∈N)