题目内容
在平面直角坐标系xOy中,已知圆x2+y2=1与x轴正半轴的交点为F,AB为该圆的一条弦,直线AB的方程为x=m.记以AB为直径的圆为⊙C,记以点F为右焦点、短半轴长为b(b>0,b为常数)的椭圆为D.
(1)求⊙C和椭圆D的标准方程;
(2)当b=1时,求证:椭圆D上任意一点都不在⊙C的内部;
(3)已知点M是椭圆D的长轴上异于顶点的任意一点,过点M且与x轴不垂直的直线交椭圆D于P、Q两点(点P在x轴上方),点P关于x轴的对称点为N,设直线QN交x轴于点L,试判断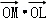 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.
(1)求⊙C和椭圆D的标准方程;
(2)当b=1时,求证:椭圆D上任意一点都不在⊙C的内部;
(3)已知点M是椭圆D的长轴上异于顶点的任意一点,过点M且与x轴不垂直的直线交椭圆D于P、Q两点(点P在x轴上方),点P关于x轴的对称点为N,设直线QN交x轴于点L,试判断
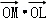 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.解:(1)圆心C(m,0),(﹣1<m<1),
则⊙C的半径为:r= ,
,
从而⊙C的方程为(x﹣m)2+y2=1﹣m2,
椭圆D的标准方程为: .
.
(2)当b=1时,椭圆D的方程为 ,
,
设椭圆D上任意一点S(x1,y1),
则 ,
, ,
,
∵ =
= =
= ≥1﹣m2=r2,
≥1﹣m2=r2,
所以SC≥r.从而椭圆D上的任意一点都不存在⊙C的内部.
(3) =b2+1为定值.
=b2+1为定值.
证明:设点P(x1,y1),Q(x2,y2),
则由题意,得N(x1,﹣y1),x1≠x2,y1≠±y2,
从而直线PQ的方程为(y2﹣y1)x﹣(x2﹣x1)y+x2y1﹣x1y2=0,
令y=0,得 ,
,
∵直线QN的方程为(y2+y1)x﹣(x2﹣x1)y﹣x1y2﹣x2y1=0,
令y=0,得 .
.
∵点P,Q在椭圆D上,
∴ ,
, ,
,
∴ ,
, ,
,
∴xM·xL= =
=
=b2+1.
∴ =xM·xL=b2+1为定值.
=xM·xL=b2+1为定值.
则⊙C的半径为:r=
 ,
,从而⊙C的方程为(x﹣m)2+y2=1﹣m2,
椭圆D的标准方程为:
 .
.(2)当b=1时,椭圆D的方程为
 ,
,设椭圆D上任意一点S(x1,y1),
则
 ,
, ,
,∵
 =
= =
= ≥1﹣m2=r2,
≥1﹣m2=r2,所以SC≥r.从而椭圆D上的任意一点都不存在⊙C的内部.
(3)
 =b2+1为定值.
=b2+1为定值.证明:设点P(x1,y1),Q(x2,y2),
则由题意,得N(x1,﹣y1),x1≠x2,y1≠±y2,
从而直线PQ的方程为(y2﹣y1)x﹣(x2﹣x1)y+x2y1﹣x1y2=0,
令y=0,得
 ,
,∵直线QN的方程为(y2+y1)x﹣(x2﹣x1)y﹣x1y2﹣x2y1=0,
令y=0,得
 .
.∵点P,Q在椭圆D上,
∴
 ,
, ,
,∴
 ,
, ,
,∴xM·xL=
 =
=
=b2+1.
∴
 =xM·xL=b2+1为定值.
=xM·xL=b2+1为定值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是