题目内容
圆x2+y2=8内有一点P(-1,2),AB为过点P但不与x轴垂直的弦,O为坐标原点.则 的取值范围________.
的取值范围________.
[-8,2]
分析:设直线AB方程为y-2=k(x+1),将它与圆方程消去y得关于x的方程,由一元二次方程根与系数关系得x1+x2=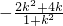 ,x1x2=
,x1x2=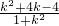 ,再结合直线方程算出y1y2=
,再结合直线方程算出y1y2=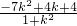 .由此得到
.由此得到 =x1x2+y1y2=-6+
=x1x2+y1y2=-6+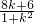 ,利用导数工具讨论关于k的函数的单调性与最值,即可得到
,利用导数工具讨论关于k的函数的单调性与最值,即可得到 的取值范围.
的取值范围.
解答:设直线AB的斜率为k,则直线AB的方程为y-2=k(x+1).
设A(x1,y1),B(x2,y2),则由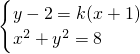 消去y,
消去y,
得(1+k2)x2+(2k2+4k)x+k2+4k-4=0
∴x1+x2=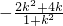 ,x1x2=
,x1x2=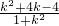
可得y1y2=[k(x1+1)+2][k(x2+1)+2]=k2x1x2+(k+2)(x1+x2)+(k+2)2=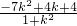 .
.
从而有 =x1x2+y1y2=
=x1x2+y1y2=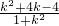 +
+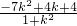 =-6+
=-6+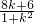
设F(k)=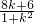 ,则F'(k)=
,则F'(k)=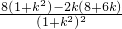 =-
=-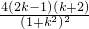
∴当k<-2或k> 时,F'(k)<0;当-2<k<
时,F'(k)<0;当-2<k< 时,F'(k)>0
时,F'(k)>0
函数F(k)在(-∞,-2)和( ,+∞)上是减函数,在(-2,
,+∞)上是减函数,在(-2, )上是增函数;
)上是增函数;
由此可得F(k)的最小值为它的极小值F(-2)=-2,最大值是它的极大值F( )=8
)=8
∴ =-6+
=-6+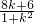 的最小值为-8,最小值为2
的最小值为-8,最小值为2
即 的取值范围为[-8,2]
的取值范围为[-8,2]
故答案为:[-8,2]
点评:本题在直线与圆相交的情况下,求数量积的取值范围,着重考查了直线与圆的位置关系和向量数量积的运算等知识,属于中档题.
分析:设直线AB方程为y-2=k(x+1),将它与圆方程消去y得关于x的方程,由一元二次方程根与系数关系得x1+x2=
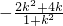 ,x1x2=
,x1x2=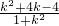 ,再结合直线方程算出y1y2=
,再结合直线方程算出y1y2=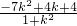 .由此得到
.由此得到 =x1x2+y1y2=-6+
=x1x2+y1y2=-6+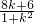 ,利用导数工具讨论关于k的函数的单调性与最值,即可得到
,利用导数工具讨论关于k的函数的单调性与最值,即可得到 的取值范围.
的取值范围.解答:设直线AB的斜率为k,则直线AB的方程为y-2=k(x+1).
设A(x1,y1),B(x2,y2),则由
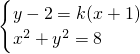 消去y,
消去y,得(1+k2)x2+(2k2+4k)x+k2+4k-4=0
∴x1+x2=
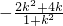 ,x1x2=
,x1x2=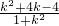
可得y1y2=[k(x1+1)+2][k(x2+1)+2]=k2x1x2+(k+2)(x1+x2)+(k+2)2=
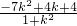 .
.从而有
 =x1x2+y1y2=
=x1x2+y1y2=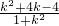 +
+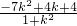 =-6+
=-6+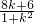
设F(k)=
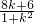 ,则F'(k)=
,则F'(k)=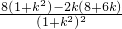 =-
=-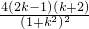
∴当k<-2或k>
 时,F'(k)<0;当-2<k<
时,F'(k)<0;当-2<k< 时,F'(k)>0
时,F'(k)>0函数F(k)在(-∞,-2)和(
 ,+∞)上是减函数,在(-2,
,+∞)上是减函数,在(-2, )上是增函数;
)上是增函数;由此可得F(k)的最小值为它的极小值F(-2)=-2,最大值是它的极大值F(
 )=8
)=8∴
 =-6+
=-6+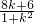 的最小值为-8,最小值为2
的最小值为-8,最小值为2即
 的取值范围为[-8,2]
的取值范围为[-8,2]故答案为:[-8,2]
点评:本题在直线与圆相交的情况下,求数量积的取值范围,着重考查了直线与圆的位置关系和向量数量积的运算等知识,属于中档题.

练习册系列答案
相关题目