题目内容
已知二次函数f(x)=x2-ax+c,(其中c>0).(1)若函数f(x)为偶函数,求a的值;
(2)当f(x)为偶函数时,若函数
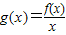 ,指出g(x)在(0,+∞)上单调性情况,并证明之.
,指出g(x)在(0,+∞)上单调性情况,并证明之.
【答案】分析:(1)若函数f(x)为偶函数,根据偶函数定义可得f(-x)=f(x),结合多项式相等的条件,求出a的值;
(2)结合(1)中结论,可得g(x)为对勾函数,利用作差法,可证明其单调性.
解答:解:(1)f(x)为偶函数,
∴f(-x)=f(x),…(2分)
即(-x)2+ax+c=x2-ax+c,
即2ax=0恒成立 …(3分)
∴a=0 …(4分)
(2)由(1),若f(x)为偶函数,则a=0,
∴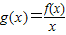 =
=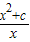 =x+
=x+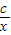 ,x∈(0,+∞)
,x∈(0,+∞)
当x∈(0,+∞)时,g(x)在x∈(0,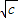 )上单调递减,在x∈(
)上单调递减,在x∈(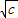 ,+∞)上单调递增,证明如下:…(5分)
,+∞)上单调递增,证明如下:…(5分)
设任意x1,x2∈(0,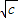 ),且x1<x2,
),且x1<x2,
g(x1)-g(x2)=(x1+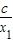 )-(x2+
)-(x2+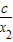 )=(x1-x2)+(
)=(x1-x2)+(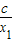 -
-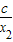 )=(x1-x2)
)=(x1-x2)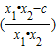 …(7分)
…(7分)
∵x1,x2∈(0,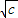 ),且x1<x2,
),且x1<x2,
∴x1-x2<0,x1•x2<c
即x1•x2-c<0
∴(x1-x2)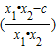 >0,
>0,
即g(x1)-g(x2)>0
即g(x1)>g(x2)
∴g(x)在(0,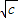 )上单调递减 …(9分)
)上单调递减 …(9分)
同理,可得g(x)在(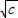 ,+∞)上单调递增 …(10分)
,+∞)上单调递增 …(10分)
点评:本题考查的知识点是函数的奇偶性,函数的单调性,其中根据函数奇偶性的定义,求出a值是解答的关键.
(2)结合(1)中结论,可得g(x)为对勾函数,利用作差法,可证明其单调性.
解答:解:(1)f(x)为偶函数,
∴f(-x)=f(x),…(2分)
即(-x)2+ax+c=x2-ax+c,
即2ax=0恒成立 …(3分)
∴a=0 …(4分)
(2)由(1),若f(x)为偶函数,则a=0,
∴
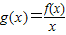 =
=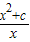 =x+
=x+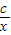 ,x∈(0,+∞)
,x∈(0,+∞)当x∈(0,+∞)时,g(x)在x∈(0,
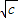 )上单调递减,在x∈(
)上单调递减,在x∈(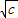 ,+∞)上单调递增,证明如下:…(5分)
,+∞)上单调递增,证明如下:…(5分)设任意x1,x2∈(0,
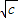 ),且x1<x2,
),且x1<x2,g(x1)-g(x2)=(x1+
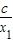 )-(x2+
)-(x2+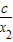 )=(x1-x2)+(
)=(x1-x2)+(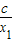 -
-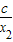 )=(x1-x2)
)=(x1-x2)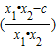 …(7分)
…(7分)∵x1,x2∈(0,
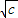 ),且x1<x2,
),且x1<x2,∴x1-x2<0,x1•x2<c
即x1•x2-c<0
∴(x1-x2)
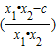 >0,
>0,即g(x1)-g(x2)>0
即g(x1)>g(x2)
∴g(x)在(0,
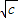 )上单调递减 …(9分)
)上单调递减 …(9分)同理,可得g(x)在(
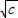 ,+∞)上单调递增 …(10分)
,+∞)上单调递增 …(10分)点评:本题考查的知识点是函数的奇偶性,函数的单调性,其中根据函数奇偶性的定义,求出a值是解答的关键.

练习册系列答案
相关题目