题目内容
已知函数f(x)=ax3+bx2+x+1(x,a,b∈R),若对任意实数x,f(x)≥0恒成立,则实数b的取值范围是________.
[ ,+∞)
,+∞)
分析:要使得f(x)≥0恒成立,结合已知函数解析式可知,只有让a=0且二次函数开口向上且与x轴没有交点,结合二次函的性质可求
解答:∵f(x)=ax3+bx2+x+1的定义域为R
当a≠0时,函数的值域为R与题意矛盾
故a=0
若使得f(x)≥0恒成立,即bx2+x+1≥0恒成立
则根据二次函数的性质可知
∴b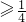
故答案为:[ ,+∞)
,+∞)
点评:本题主要考查了函数的恒成立为题的求解,解题的关键是灵活利用函数知识
 ,+∞)
,+∞)分析:要使得f(x)≥0恒成立,结合已知函数解析式可知,只有让a=0且二次函数开口向上且与x轴没有交点,结合二次函的性质可求
解答:∵f(x)=ax3+bx2+x+1的定义域为R
当a≠0时,函数的值域为R与题意矛盾
故a=0
若使得f(x)≥0恒成立,即bx2+x+1≥0恒成立
则根据二次函数的性质可知

∴b
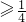
故答案为:[
 ,+∞)
,+∞)点评:本题主要考查了函数的恒成立为题的求解,解题的关键是灵活利用函数知识

练习册系列答案
相关题目