题目内容
若直线y=2与曲线y=x2-|x|+a有两个交点,则a的取值范围是分析:在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a的图象,观察求解.
解答: 解:如图,在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a,
解:如图,在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a,
观图可知,a的取值必须满足{a|a<2或a=
},
故答案为{a|a<2或a=
}
 解:如图,在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a,
解:如图,在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a,观图可知,a的取值必须满足{a|a<2或a=
| 9 |
| 4 |
故答案为{a|a<2或a=
| 9 |
| 4 |
点评:本小题主要考查函数的图象与性质、不等式的解法,着重考查了数形结合的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
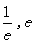 ]有公共点,求t的取值范围,
]有公共点,求t的取值范围, 有两个交点,则
有两个交点,则 的取值范围是
的取值范围是