题目内容
8．若a，b，c均为正实数，则三个数a+$\frac{1}{b}$，b+$\frac{1}{c}$，c+$\frac{1}{a}$这三个数中不小于2的数（ ）| A． | 可以不存在 | B． | 至少有1个 | C． | 至少有2个 | D． | 至多有2个 |
分析 根据基本不等式，利用反证法思想，可以确定至少有一个不小于2，从而可以得结论．
解答 解：假设a+$\frac{1}{b}$，b+$\frac{1}{c}$，c+$\frac{1}{a}$这三个数都小于2，
∴a+$\frac{1}{b}$+b+$\frac{1}{c}$+c+$\frac{1}{a}$＜6
∵a+$\frac{1}{b}$+b+$\frac{1}{c}$+c+$\frac{1}{a}$=（a+$\frac{1}{a}$）+（b+$\frac{1}{b}$）+（c+$\frac{1}{c}$）≥2+2+2=6，
这与假设矛盾，
故至少有一个不小于2
故选：B
点评 本题的考点是不等式的大小比较，考查基本不等式的运用，考查了反证法思想，难度不大
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
16．已知函数f（x）=x（1+|x|），设关于x的不等式f（x2+1）＞f（ax）的解集为A，若$[-\frac{1}{2}，\frac{1}{2}]⊆A$，则实数a的取值范围为（ ）
| A． | （-2，2） | B． | $（-\frac{5}{2}，\frac{5}{2}）$ | C． | $（-\frac{5}{2}，-1）∪（1，\frac{5}{2}）$ | D． | $（-∞，-\frac{5}{2}）∪（\frac{5}{2}，+∞）$ |
20．函数f（x）=x2+cosx的导数f′（x）为（ ）
| A． | x-sinx | B． | 2x-sinx | C． | x+sinx | D． | 2x+sinx |
17．
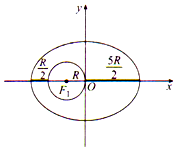我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后，在地球轨道上经历3次调相轨道变轨，奔向月球，进入月球轨道，“嫦娥一号”轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点，远地点离地面的距离分别是$\frac{R}{2}$，$\frac{5R}{2}$（如图所示），则“嫦娥一号”卫星轨道的离心率为（ ）| A． | $\frac{2}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |