题目内容
【题目】设函数![]() ,其中
,其中![]() ,
,![]()
(1)若![]() ,且
,且![]() 是
是![]() 的极大值点,求
的极大值点,求![]() 的取值范围;
的取值范围;
(2)当![]() ,
,![]() 时,方程
时,方程![]() 有唯一实数根,求正数
有唯一实数根,求正数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() ,知
,知![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,故
,故![]() .由此能求出
.由此能求出![]() 的取值范围.
的取值范围.
(2)由方程![]() 有唯一实数解,知
有唯一实数解,知![]() 有唯一实数解,设
有唯一实数解,设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() .由此入手能够推导出正数
.由此入手能够推导出正数![]() 的值.
的值.
解:(1)∵![]() ,其中
,其中![]() ,
,![]()
∴![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() .
.
①若![]() ,由
,由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,所以
单调递减,所以![]() 是
是![]() 的极大值点.
的极大值点.
②若![]() ,则
,则![]() ,得
,得![]() ,或
,或![]() ,∵
,∵![]() 是
是![]() 的极大值点,
的极大值点,
∴![]() ,解得
,解得![]() .
.
综合①②,得![]() 的取值范围是
的取值范围是![]() .
.
(2)∵方程![]() 中唯一实数解,∴
中唯一实数解,∴![]() 有唯一实数解,
有唯一实数解,
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() .∵
.∵![]() ,∴
,∴![]() ,
,
方程有两异号根![]() ,设
,设![]() ,∵
,∵![]() ,∴
,∴![]() 应舍去.
应舍去.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() 取最小值
取最小值![]() .
.
∵![]() 有唯一解,∴
有唯一解,∴![]() ,
,
则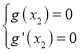 ,即
,即 ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() (*),
(*),
设函数![]() ,∵当
,∵当![]() 时,
时,![]() 是增函数,
是增函数,
∴![]() 至多有一解,∵
至多有一解,∵![]() ,∴方程(*)的解为
,∴方程(*)的解为![]() ,
,
代入方程组解得![]() .
.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目