题目内容
已知函数f(x)=ax-21nx,a∈R
(Ⅰ)a=1时,求函数f(x)的极值;
(Ⅱ)求f(x)单调区间
(Ⅲ)设 ,若在[1,e]上至少存在一个x0,使得f(x0)>g(x0)成立,求实数a的取值范围.
,若在[1,e]上至少存在一个x0,使得f(x0)>g(x0)成立,求实数a的取值范围.
解:(I) .令f'(x)=0,得x=2
.令f'(x)=0,得x=2
当x变化时,f'(x)与f(x)变化情况如下表:
∴当x=2时,f(x)取得极小值f(2)=2-2ln2.
(Ⅱ)a≤0时,f(x)在(0,+∞)上为减函数;a>0时,f(x)在(0, )上是减函数,
)上是减函数,
在( )上是增函数.
)上是增函数.
(Ⅲ)本命题等价于f(x)-g(x)>0在[1,e]上有解,设F(x)=f(x)-g(x)=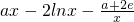 ,
,
F'(x)=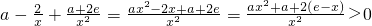 ,
,
所以F(x)为增函数,F(x)max=F(e).
依题意需F(e)>0,解得 .所以a的取值范围是
.所以a的取值范围是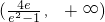 .
.
分析:(I)由题意对函数求导,然后解f′(x)=0方程,得到x=2,将(0,+∞)分为二个区间,最后通过列表得出导数在这二个区间的符号,讨论出函数的单调性,即可得出函数的极值.
(II)先求导数fˊ(x),求出f′(x)=0的值,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,从而的函数f(x)的单调区间以及函数的极值,fˊ(x)>0的区间是增区间,fˊ(x)<0的区间是减区间.
(III)本命题等价于f(x)-g(x)>0在[1,e]上有解,设F(x)=f(x)-g(x)=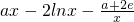 ,求导:
,求导:
F'(x)=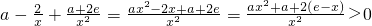 ,得出F(x)max=F(e).
,得出F(x)max=F(e).
依题意需F(e)>0,从而求得a的取值范围.
点评:本题主要考查了函数的极值,以及利用导数研究函数的单调性等基础知识,考查综合利用数学知识分析问题、解决问题的能力.
 .令f'(x)=0,得x=2
.令f'(x)=0,得x=2当x变化时,f'(x)与f(x)变化情况如下表:
| x | (0,2) | 2 | (2,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
(Ⅱ)a≤0时,f(x)在(0,+∞)上为减函数;a>0时,f(x)在(0,
 )上是减函数,
)上是减函数,在(
 )上是增函数.
)上是增函数.(Ⅲ)本命题等价于f(x)-g(x)>0在[1,e]上有解,设F(x)=f(x)-g(x)=
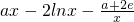 ,
,F'(x)=
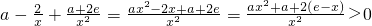 ,
,所以F(x)为增函数,F(x)max=F(e).
依题意需F(e)>0,解得
 .所以a的取值范围是
.所以a的取值范围是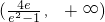 .
.分析:(I)由题意对函数求导,然后解f′(x)=0方程,得到x=2,将(0,+∞)分为二个区间,最后通过列表得出导数在这二个区间的符号,讨论出函数的单调性,即可得出函数的极值.
(II)先求导数fˊ(x),求出f′(x)=0的值,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,从而的函数f(x)的单调区间以及函数的极值,fˊ(x)>0的区间是增区间,fˊ(x)<0的区间是减区间.
(III)本命题等价于f(x)-g(x)>0在[1,e]上有解,设F(x)=f(x)-g(x)=
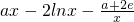 ,求导:
,求导:F'(x)=
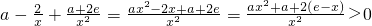 ,得出F(x)max=F(e).
,得出F(x)max=F(e).依题意需F(e)>0,从而求得a的取值范围.
点评:本题主要考查了函数的极值,以及利用导数研究函数的单调性等基础知识,考查综合利用数学知识分析问题、解决问题的能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目