Question

下列函数中，既是奇函数又是增函数的为（　　）

A．

y=x+1

B．

y=﹣x2

C．

D．

y=x|x|

Answer 1

考点：

函数奇偶性的判断；函数单调性的判断与证明．

专题：

探究型．

分析：

对于A，非奇非偶；对于B，是偶函数；对于C，是奇函数，但不是增函数；

对于D，令f（x）=x|x|=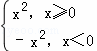，可判断函数既是奇函数又是增函数，故可得结论．

解答：

解：对于A，非奇非偶，是R上的增函数，不符合题意；

对于B，是偶函数，不符合题意；

对于C，是奇函数，但不是增函数；

对于D，令f（x）=x|x|，∴f（﹣x）=﹣x|﹣x|=﹣f（x）；∵f（x）=x|x|=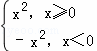，∴函数是增函数

故选D．

点评：

本题考查函数的性质，考查函数的奇偶性与单调性的判断，属于基础题．