题目内容
设O点在△ABC内部,且有 ,则△ABC的面积与△AOC的面积的比为
,则△ABC的面积与△AOC的面积的比为
- A.2
- B.

- C.3
- D.

C
分析:根据 ,变形得∴
,变形得∴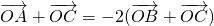 ,利用向量加法的平行四边形法则可得2
,利用向量加法的平行四边形法则可得2  =-4
=-4  ,从而确定点O的位置,进而求得△ABC 的面积与△AOC 的面积的比.
,从而确定点O的位置,进而求得△ABC 的面积与△AOC 的面积的比.
解答: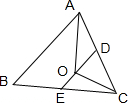 解:分别取AC、BC的中点D、E,
解:分别取AC、BC的中点D、E,
∵ ,
,
∴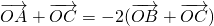 ,即2
,即2  =-4
=-4  ,
,
∴O是DE的一个三等分点,
∴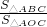 =3,
=3,
故选C.
点评:此题是个基础题.考查向量在几何中的应用,以及向量加法的平行四边形法则和向量共线定理等基础知识,同时考查学生灵活应用知识分析解决问题的能力和计算能力.
分析:根据
 ,变形得∴
,变形得∴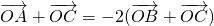 ,利用向量加法的平行四边形法则可得2
,利用向量加法的平行四边形法则可得2  =-4
=-4  ,从而确定点O的位置,进而求得△ABC 的面积与△AOC 的面积的比.
,从而确定点O的位置,进而求得△ABC 的面积与△AOC 的面积的比.解答:
 解:分别取AC、BC的中点D、E,
解:分别取AC、BC的中点D、E,∵
 ,
,∴
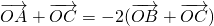 ,即2
,即2  =-4
=-4  ,
,∴O是DE的一个三等分点,
∴
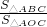 =3,
=3,故选C.
点评:此题是个基础题.考查向量在几何中的应用,以及向量加法的平行四边形法则和向量共线定理等基础知识,同时考查学生灵活应用知识分析解决问题的能力和计算能力.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
设 O点 在△ABC内部,且有
+2
+3
=
,则△ABC 的面积与△AOC 的面积的比为( )
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
设O点在△ABC内部,且有
+2
+3
=
,则△ABC的面积与△AOC的面积的比为( )
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
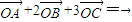 ,则△ABC 的面积与△AOC 的面积的比为( )
,则△ABC 的面积与△AOC 的面积的比为( )
