题目内容
为了了解某小区2000户居民月用水量使用情况,通过随机抽样获得了100户居民的月用水量.下图是调查结果的频率分布直方图.
(1)做出样本数据的频率分布折线图;
(2)并根据频率直方图估计某小区2000户居民月用水量使用大于3的户数;
(3)利用频率分布直方图估计该样本的平均数和中位数(保留到0.001)
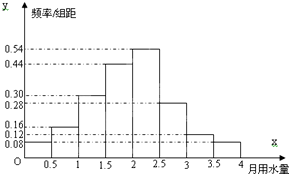
(1)做出样本数据的频率分布折线图;
(2)并根据频率直方图估计某小区2000户居民月用水量使用大于3的户数;
(3)利用频率分布直方图估计该样本的平均数和中位数(保留到0.001)

分析:(1)连接每个小矩形上底边的中点得出频率分布折线图
(2)居民月用水量使用大于3的户数的频率为最左边两个矩形的面积之和.再乘以2000即可.
(3)由频率分布直方图估计样本数据的中位数,平均数,规律是:中位数,出现在在概率是0.5的地方,平均数为每个矩形的面积与底边中点乘积之和.
(2)居民月用水量使用大于3的户数的频率为最左边两个矩形的面积之和.再乘以2000即可.
(3)由频率分布直方图估计样本数据的中位数,平均数,规律是:中位数,出现在在概率是0.5的地方,平均数为每个矩形的面积与底边中点乘积之和.
解答:解:(1)①频率分布折线图如图所示:
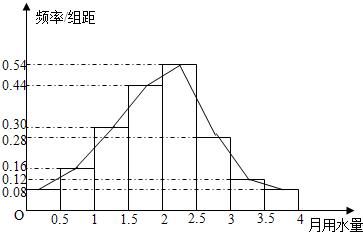
②∵样本中居民月用水量在3-3.5的频率f=0.12×0.5=0.06
∵样本中居民月用水量在3.5-4的频率f=0.08×0.5=0.04
∴样本中居民月用水量大于3的频率为0.06×0.04=0.1(人)
所以某小区2000户居民月用水量使用大于3的户数为2000×(0.1)=200
①
=(0.08×0.25+0.16×0.75+0.30×1.5+0.44×1.75+0.54×2.25+0.28×2.75+0.12×3.25+0.08×3.75)×0.5=1.98
左边四个小矩形的面积之和为0.04+0.08+0.15+0.22=0.49,
要达到频率为0.5,需第五个矩形的面积为0.01,需要底边长为0.01÷0.54≈0.0185
所以中位数为2+0.0185=2.0185.

②∵样本中居民月用水量在3-3.5的频率f=0.12×0.5=0.06
∵样本中居民月用水量在3.5-4的频率f=0.08×0.5=0.04
∴样本中居民月用水量大于3的频率为0.06×0.04=0.1(人)
所以某小区2000户居民月用水量使用大于3的户数为2000×(0.1)=200
①
. |
| x |
左边四个小矩形的面积之和为0.04+0.08+0.15+0.22=0.49,
要达到频率为0.5,需第五个矩形的面积为0.01,需要底边长为0.01÷0.54≈0.0185
所以中位数为2+0.0185=2.0185.
点评:用样本估计总体,是研究统计问题的一个基本思想方法,频率分布直方图中小长方形的面积=频率,各个矩形面积之和等于1,能根据直方图求众数和中位数,平均数.属于常规题型.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目