题目内容
双曲线x2-y2=8的左右焦点分别为F1,F2,点Pn(xn,yn)(n=1,2,3…)在其右支上,且满足|Pn+1F2|=|PnF1|,P1F2⊥F1F2,则x2012的值是
- A.8040

- B.80484

- C.8048
- D.8040
C
分析:根据题意可求得P1点的横坐标x1(就是右焦点F2的横坐标),利用两点间的距离公式由|Pn+1F2|=|PnF1|可求得xn+1-xn=4,从而利用等差数列的通项公式即可求得x2012的值.
解答:∵a2=8,b2=8,
∴c=4,即x1=4,又|Pn+1F2|=|PnF1|,
∴ +
+ =
= +
+ ,
,
即 -8xn+1+16+
-8xn+1+16+ =
=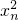 +8xn+16+
+8xn+16+ ,
,
∴(xn+1+xn)(xn+1-xn-4)=0,
由题意知,xn>0,
∴xn+1-xn=4,
∴{xn}是以4为首项,4为公差的等差数列,
∴x2012=x1+2011×4=4+8044=8048.
故选C.
点评:本题考查双曲线的简单性质,突出考查等差数列的通项公式,通过分析运算得到xn+1-xn=4是关键,也是难点,奥差化归思想与运算能力,属于中档题.
分析:根据题意可求得P1点的横坐标x1(就是右焦点F2的横坐标),利用两点间的距离公式由|Pn+1F2|=|PnF1|可求得xn+1-xn=4,从而利用等差数列的通项公式即可求得x2012的值.
解答:∵a2=8,b2=8,
∴c=4,即x1=4,又|Pn+1F2|=|PnF1|,
∴
 +
+ =
= +
+ ,
,即
 -8xn+1+16+
-8xn+1+16+ =
=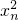 +8xn+16+
+8xn+16+ ,
,∴(xn+1+xn)(xn+1-xn-4)=0,
由题意知,xn>0,
∴xn+1-xn=4,
∴{xn}是以4为首项,4为公差的等差数列,
∴x2012=x1+2011×4=4+8044=8048.
故选C.
点评:本题考查双曲线的简单性质,突出考查等差数列的通项公式,通过分析运算得到xn+1-xn=4是关键,也是难点,奥差化归思想与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在双曲线x2-y2=8的右支上过右焦点F2的一条弦PQ,|PQ|=7,F1是左焦点,那么△F1PQ的周长为( )
| A、28 | ||
B、8
| ||
C、14-8
| ||
D、14+8
|