题目内容
三棱锥S-ABC中,侧棱SA、SB、SC两两互相垂直,M为三角形ABC的重心,D为AB的中点,作与SC平行的直线DP.
证明:
(1)DP与SM相交;
(2)设DP与SM的交点为D′,则D′为三棱锥S-ABC的外接球球心.
证明:
(1)DP与SM相交;
(2)设DP与SM的交点为D′,则D′为三棱锥S-ABC的外接球球心.
分析:(1)由DP∥SC,可得DP、SC共面,于是DC在此平面内,所以点M在此平面内.再由SM与SC相交,则SM必与DP相交.
(2)由已知侧棱SA、SB、SC两两互相垂直及SC∥DD′,可证得直角梯形SCD′D,若取SC的中点Q,再由DD′∥SC及MC=2DM,得SC=2DD′及矩形SQDD′,于是可得SD′=CD′.同理可得D′A=D′B=D′S,于是证得结论.
(2)由已知侧棱SA、SB、SC两两互相垂直及SC∥DD′,可证得直角梯形SCD′D,若取SC的中点Q,再由DD′∥SC及MC=2DM,得SC=2DD′及矩形SQDD′,于是可得SD′=CD′.同理可得D′A=D′B=D′S,于是证得结论.
解答: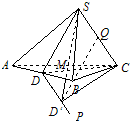 证明:(1)∵DP∥SC,故DP、CS共面.
证明:(1)∵DP∥SC,故DP、CS共面.
∴DC?面DPC,
∵M∈DC,∴M∈面DPC,∴SM?面DPC.
∵在面DPC内SM与SC相交,故直线SM与DP相交.
(2)∵SA、SB、SC两两互相垂直,∴SC⊥面SAB,∴SC⊥SD.
∵DP∥SC,∴DP⊥SD,△DD′M∽△CSM.
∵M为△ABC的重心,∴DM:MC=1:2.∴DD′:SC=1:2.
取SC中点Q,连D′Q.则SQ=DD′,
∴SQ
DD′,SC⊥SD,
∴平面四边形DD′QS是矩形.
∴D′Q⊥SC,又SQ=QC,知D′C=D′S.
同理,D′A=D′B=D′C=D′S.
即以D′为球心D′S为半径作球D′,则A、B、C均在此球上.
即D′为三棱锥S-ABC的外接球球心.
 证明:(1)∵DP∥SC,故DP、CS共面.
证明:(1)∵DP∥SC,故DP、CS共面.∴DC?面DPC,
∵M∈DC,∴M∈面DPC,∴SM?面DPC.
∵在面DPC内SM与SC相交,故直线SM与DP相交.
(2)∵SA、SB、SC两两互相垂直,∴SC⊥面SAB,∴SC⊥SD.
∵DP∥SC,∴DP⊥SD,△DD′M∽△CSM.
∵M为△ABC的重心,∴DM:MC=1:2.∴DD′:SC=1:2.
取SC中点Q,连D′Q.则SQ=DD′,
∴SQ
| ∥ |
. |
∴平面四边形DD′QS是矩形.
∴D′Q⊥SC,又SQ=QC,知D′C=D′S.
同理,D′A=D′B=D′C=D′S.
即以D′为球心D′S为半径作球D′,则A、B、C均在此球上.
即D′为三棱锥S-ABC的外接球球心.
点评:本题综合考查了线线共面、线面垂直、线线平行的性质、等腰三角形的性质、矩形及点共球等,深刻理解以上判定及性质是解决问题的关键.

练习册系列答案
相关题目
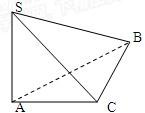 如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,
如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,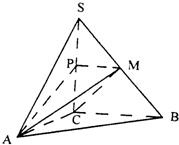 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°. 如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形,
如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形, 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2