题目内容
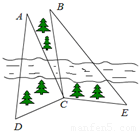
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).(1)求△CDE的面积;
(2)求A,B之间的距离.
【答案】分析:(1)连接DE,在△CDE中,求出∠DCE,直接利用三角形的面积公式求解即可.
(2)求出AC,通过正弦定理求出BC,然后利用余弦定理求出AB.
解答:解:(1)连接DE,在△CDE中,∠DCE=360°-90°-15°-105°=150°,(1分)
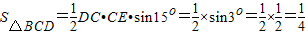 (平方百米) (4分)
(平方百米) (4分)
(2)依题意知,在RT△ACD中,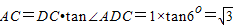 (5分)
(5分)
在△BCE中,∠CBE=180°-∠BCE-∠CEB=180°-105°-45°=30°
由正弦定理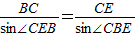 (6分)
(6分)
得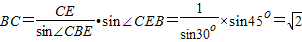 (7分)
(7分)
∵cos15°=cos(60-45°)=cos60°cos45°+sin60°sin45° (8分)
=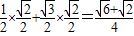 (9分)
(9分)
在△ABC中,由余弦定理AB2=AC2+BC2-2AC•BCcos∠ACB (10分)
可得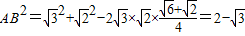 (11分)
(11分)
∴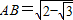 (百米) (12分)
(百米) (12分)
点评:本题考查三角形的面积的求法,正弦定理与余弦定理的应用,考查计算能力.
(2)求出AC,通过正弦定理求出BC,然后利用余弦定理求出AB.
解答:解:(1)连接DE,在△CDE中,∠DCE=360°-90°-15°-105°=150°,(1分)
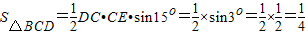 (平方百米) (4分)
(平方百米) (4分)(2)依题意知,在RT△ACD中,
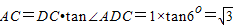 (5分)
(5分)在△BCE中,∠CBE=180°-∠BCE-∠CEB=180°-105°-45°=30°
由正弦定理
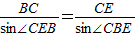 (6分)
(6分)得
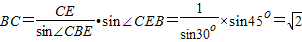 (7分)
(7分)∵cos15°=cos(60-45°)=cos60°cos45°+sin60°sin45° (8分)
=
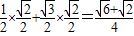 (9分)
(9分)在△ABC中,由余弦定理AB2=AC2+BC2-2AC•BCcos∠ACB (10分)
可得
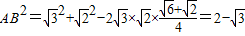 (11分)
(11分)∴
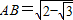 (百米) (12分)
(百米) (12分)点评:本题考查三角形的面积的求法,正弦定理与余弦定理的应用,考查计算能力.

练习册系列答案
相关题目
一般来说,一个人脚掌越长,他的身高就越高,现对10名成年人的脚掌长 与身高
与身高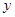 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为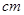 )如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据:
)如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据: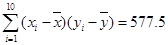 ,
,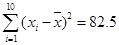 ;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为
;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为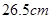 ,则估计案发嫌疑人的身高为
,则估计案发嫌疑人的身高为
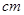 .
.
|
脚长 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
身高 |
141 |
146 |
154 |
160 |
169 |
176 |
181 |
188 |
197 |
203 |