题目内容
(本小题满分12分)已知定义在 上的函数
上的函数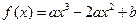
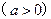 在区间
在区间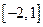 上的最大值是
上的最大值是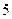 ,最小值是
,最小值是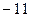 .
.
(1)求函数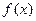 的解析式;
的解析式;
(2)若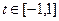 时,
时,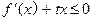 恒成立,求实数
恒成立,求实数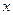 的取值范围.
的取值范围.
 上的函数
上的函数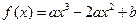
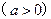 在区间
在区间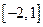 上的最大值是
上的最大值是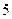 ,最小值是
,最小值是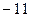 .
.(1)求函数
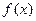 的解析式;
的解析式;(2)若
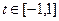 时,
时,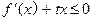 恒成立,求实数
恒成立,求实数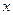 的取值范围.
的取值范围.(1) ;(2)[0,1].
;(2)[0,1].
 ;(2)[0,1].
;(2)[0,1].解:(1)
令 =0,得
=0,得 ………2分
………2分
因为 ,所以可得下表:
,所以可得下表:
………………4分
因此 必为最大值,∴
必为最大值,∴ ,因此
,因此 ,
,
 ,
,
即 ,∴
,∴ ,
,
∴ ……………6分
……………6分
(2)∵ ,∴
,∴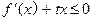 等价于
等价于 , ………8分
, ………8分
令 ,则问题就是
,则问题就是 在
在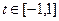 上恒成立时,求实数
上恒成立时,求实数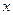 的取值范围,为此只需
的取值范围,为此只需 ,即
,即 , …………10分
, …………10分
解得 ,所以所求实数
,所以所求实数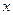 的取值范围是[0,1]. ………………12分
的取值范围是[0,1]. ………………12分

令
 =0,得
=0,得 ………2分
………2分因为
 ,所以可得下表:
,所以可得下表: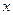 |  | 0 |  |
 | + | 0 | - |
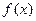 | ↗ | 极大 | ↘ |
因此
 必为最大值,∴
必为最大值,∴ ,因此
,因此 ,
,  ,
,即
 ,∴
,∴ ,
,∴
 ……………6分
……………6分(2)∵
 ,∴
,∴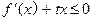 等价于
等价于 , ………8分
, ………8分令
 ,则问题就是
,则问题就是 在
在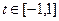 上恒成立时,求实数
上恒成立时,求实数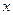 的取值范围,为此只需
的取值范围,为此只需 ,即
,即 , …………10分
, …………10分解得
 ,所以所求实数
,所以所求实数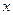 的取值范围是[0,1]. ………………12分
的取值范围是[0,1]. ………………12分
练习册系列答案
相关题目
 ,
, ,
, ,则a,b,c三个数的大小关系是
,则a,b,c三个数的大小关系是



 的一个单调递减区间是( )
的一个单调递减区间是( )
 )
) ]
] ]
]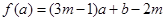 ,当
,当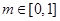 时,
时,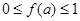 恒成立,则
恒成立,则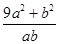

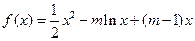 ,
,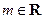 .
.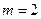 时,求函数
时,求函数 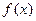 的最小值;
的最小值;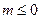 时,讨论函数
时,讨论函数 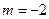 时,对任意的
时,对任意的 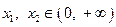 ,且
,且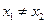 ,有
,有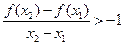 .
.
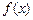 与产量
与产量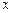 之间的关系式为
之间的关系式为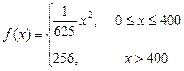 ,每件产品的售价
,每件产品的售价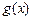 与产量
与产量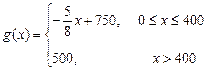 .
.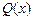 与产量
与产量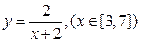 则函数的最大值为__,最小值为_____
则函数的最大值为__,最小值为_____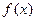 的图像经过点
的图像经过点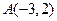 、
、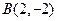 ,若函数
,若函数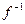 (
(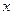 ),则不等式
),则不等式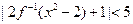 的解集为 。
的解集为 。