题目内容
已知曲线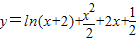 在点A处的切线与曲线
在点A处的切线与曲线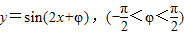 在点B处的切线相同,求φ的值.
在点B处的切线相同,求φ的值.
【答案】分析:分别求出两函数的导函数,根据导函数的取值范围可求出切线的斜率,从而求出切线方程,然后根据曲线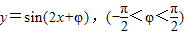 在点B处的切线相同,可求出φ的值.
在点B处的切线相同,可求出φ的值.
解答:解:k切=y′=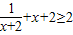 ,当且仅当x+2=
,当且仅当x+2=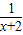 ,即x+2=1,x=-1时,取等号…(2分)
,即x+2=1,x=-1时,取等号…(2分)
又k切=y′=2cos(2x+ϕ)≤2,
由题意,k切=2,此时切点A(-1,-1),切线l:y=2x+1…(5分)
由2cos(2x+ϕ)=2得cos(2x+ϕ)=1,
∴sin(2x+ϕ)=0,从而B(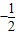 ,0)…(7分)
,0)…(7分)
∴sin(-1+ϕ)=0,-1+ϕ=kπ,k∈Z,
∴ϕ=kπ+1,k∈Z…(9分)
又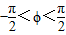 ,
,
∴ϕ=1
点评:本题主要考查了利用导数研究曲线上某点的切线方程,同时考查了转化的思想和运算求解的能力,属于中档题.
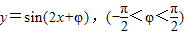 在点B处的切线相同,可求出φ的值.
在点B处的切线相同,可求出φ的值.解答:解:k切=y′=
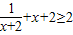 ,当且仅当x+2=
,当且仅当x+2=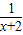 ,即x+2=1,x=-1时,取等号…(2分)
,即x+2=1,x=-1时,取等号…(2分)又k切=y′=2cos(2x+ϕ)≤2,
由题意,k切=2,此时切点A(-1,-1),切线l:y=2x+1…(5分)
由2cos(2x+ϕ)=2得cos(2x+ϕ)=1,
∴sin(2x+ϕ)=0,从而B(
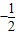 ,0)…(7分)
,0)…(7分)∴sin(-1+ϕ)=0,-1+ϕ=kπ,k∈Z,
∴ϕ=kπ+1,k∈Z…(9分)
又
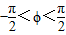 ,
,∴ϕ=1
点评:本题主要考查了利用导数研究曲线上某点的切线方程,同时考查了转化的思想和运算求解的能力,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目