题目内容
以下结论正确的是
- A.命题“对边平行且相等的四边形是平行四边形”不是全称命题
- B.命题“?x∈R,x2+x+4≤0”的否定是“?x∈R,x2+x+4≥0”
- C.“a=b”是“ac=bc”的必要不充分条件
- D.“a+5是无理数”是“a是无理数”的充要条件
D
分析:本题考查的知识点是必要条件、充分条件与充要条件的判断及不等式的性质,我们根据充要条件的定义对题目中的四个答案逐一进行分析即可得到答案.
解答:对于A:命题“对边平行且相等的四边形是平行四边形”是全称命题,故错;
对于B:∵对命题“?x∈A,P(X)”的否定是:“?x∈A,?P(X)”
∴对命题“?x∈R,x2+x+4≤0”的否定是“?x∈R,x2+x+4<0”
故错;
∵C中“a=b”?“ac=bc”为真命题,
但当c=0时,“ac=bc”?“a=b”为假命题,
故“a=b”是“ac=bc”的充分不必要条件,故C为假命题;
∵D中“a+5是无理数”?“a是无理数”为真命题,
“a是无理数”?“a+5是无理数”也为真命题,
故“a+5是无理数”是“a是无理数”的充要条件,故D为真命题;
故选D.
点评:判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
分析:本题考查的知识点是必要条件、充分条件与充要条件的判断及不等式的性质,我们根据充要条件的定义对题目中的四个答案逐一进行分析即可得到答案.
解答:对于A:命题“对边平行且相等的四边形是平行四边形”是全称命题,故错;
对于B:∵对命题“?x∈A,P(X)”的否定是:“?x∈A,?P(X)”
∴对命题“?x∈R,x2+x+4≤0”的否定是“?x∈R,x2+x+4<0”
故错;
∵C中“a=b”?“ac=bc”为真命题,
但当c=0时,“ac=bc”?“a=b”为假命题,
故“a=b”是“ac=bc”的充分不必要条件,故C为假命题;
∵D中“a+5是无理数”?“a是无理数”为真命题,
“a是无理数”?“a+5是无理数”也为真命题,
故“a+5是无理数”是“a是无理数”的充要条件,故D为真命题;
故选D.
点评:判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 是平面,
是平面, 是直线,则以下结论正确的是
是直线,则以下结论正确的是 ,则
,则 B. 若
B. 若 ,则
,则
 ,则
,则 D. 若
D. 若 ,则
,则
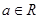 ,函数
,函数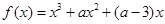 的导函数是
的导函数是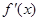 ,若
,若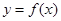 的极大值为
的极大值为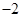 B.
B.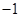
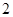 D.
D.