题目内容
手表的表面在一平面上.整点1,2,…,12这12个数字等间隔地分布在半径为1的圆周上.从整点i到整点i+1的向量记作
,则
•
+
•
+…+
•
=______.
| titi+1 |
| t1t2 |
| t2t3 |
| t2t3 |
| t3t4 |
| t12t1 |
| t1t2 |
:∵整点把圆分成12份,
∴每一份所对应的圆心角是30度,
连接相邻的两点组成等腰三角形底边平方为 2-
,每对向量的夹角为30°,
每对向量的数量积为 ( 2-
)cos30°=
-
,故
•
+
•
+…+
•
=12(
-
)=12
-18,
故答案为 12
-18.
∴每一份所对应的圆心角是30度,
连接相邻的两点组成等腰三角形底边平方为 2-
| 3 |
每对向量的数量积为 ( 2-
| 3 |
| 3 |
| 3 |
| 2 |
| t1t2 |
| t2t3 |
| t2t3 |
| t3t4 |
| t12t1 |
| t1t2 |
| 3 |
| 3 |
| 2 |
| 3 |
故答案为 12
| 3 |

练习册系列答案
相关题目
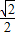 的圆周上,从整点i到整点(i+1)的向量记作
的圆周上,从整点i到整点(i+1)的向量记作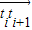 ,则
,则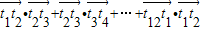 = .
= .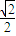 的圆周上,从整点i到整点(i+1)的向量记作
的圆周上,从整点i到整点(i+1)的向量记作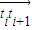 ,则
,则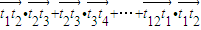 = .
= .