题目内容
【题目】过抛物线y2=2px(p>0)焦点F的直线与抛物线交于A,B两点,作AC,BD垂直抛物线的准线l于C,D,其中O为坐标原点,则下列结论正确的是 . (填序号)
① ![]() ;
;
②存在λ∈R,使得 ![]() 成立;
成立;
③ ![]() =0;
=0;
④准线l上任意一点M,都使得 ![]() >0.
>0.
【答案】①②③
【解析】解:对于①,由 ![]() ,可得①正确;
,可得①正确;
对于②,设A(x1 , y1),B(x2 , y2),可得C(﹣ ![]() ,y1),D(﹣
,y1),D(﹣ ![]() ,y2),
,y2),
又kOA= ![]() =
= ![]() ,kAD=
,kAD= ![]() ,设直线AB方程为x=my+
,设直线AB方程为x=my+ ![]() .
.
代入抛物线的方程,可得y2﹣2pmy﹣p2=0,
可得y1y2=﹣p2 , 即有y1(y1﹣y2)=y12﹣y1y2=2px1+p2 ,
则kOA=kAD , 即有存在λ∈R,使得 ![]() 成立,则②正确;
成立,则②正确;
对于③, ![]() =(﹣p,y1)(﹣p,y2)=y1y2+p2=0,可得③正确;
=(﹣p,y1)(﹣p,y2)=y1y2+p2=0,可得③正确;
对于④,由抛物线的定义可得|AB|=|AC|+|BD|,
可得以AB为直径的圆的半径与梯形ACDB的中位线长相等,
即有该圆与CD相切,设切点为M,即有AM⊥BM,则 ![]() =0,
=0,
则④不正确.
所以答案是:①②③.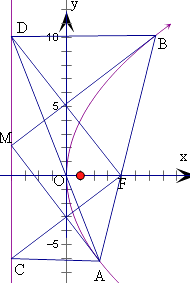

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目