Question

若n是3的倍数,求证:3ⁿ-1是13的倍数.

Answer 1

解析：为寻求3ⁿ-1与13的关系,可先用n的几个特殊值代入验证,以发现解题思路.?

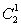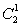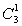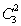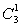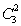如3³-1=27-1=26;3⁶-1=(26+1)²-1=26²+·26+1-1=26(26+);3⁹-1=(26+1)³-1=26³+·26²+·26+26+1-1=26(26²+·26++1).?

因此,只要令n=3k,将3ⁿ-1改写为27^k-1,再将27改写为26+1,作二项式展开即可.

证明：令n=3k,k是整数,则3ⁿ-1=27^k-1=(26+1)^k-1=26^k+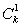·26^k-1+…+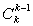·26+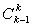=26(26^k-1+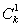·26^k-2+…+).?

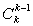因为(26^k-1+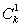·26^k-2+…+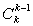)是整数,?

所以3ⁿ-1是13的倍数.