题目内容
已知数列{an}是等差数列,a2=6,a5=18,数列{bn}的前n项和为Tn,且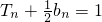 .
.
(Ⅰ)求数列{an}的通项公式及其前n项和Mn;
(Ⅱ)求证数列{bn}是等比数列,并求出其通项公式与前n项和Tn公式;
(III)记cn=an•bn,求数列{cn}的前n项和Sn.
解:(Ⅰ)设数列{an}的公差为d,
由a2=6,a5=18,
可得a1+d=6,a1+4d=18,
解得a1=2,d=4.
从而an=4n-2,Mn=2n2
(Ⅱ)由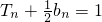 ,
,
令n=1,则 ,可得
,可得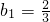 .
.
当n≥2时,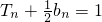 ,
, ,
,
两式相减得 .
.
可得 .
.
所以数列{bn}是等比数列.
可得 ,
, .…(8分)
.…(8分)
(Ⅲ)由 .
.
则 .
. .
.
两式相减得 .
.
整理得
分析:(Ⅰ)设数列{an}的公差为d,由a2=6,a5=18,可求首项及公差,进而可求通项公式及前n项和
(Ⅱ)由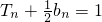 ,令n=1,可求
,令n=1,可求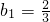 .当n≥2时,由
.当n≥2时,由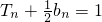 ,可得
,可得 ,两式相减得
,两式相减得 .即
.即 ,利用等比数列的通项公式及前n项和公式可求
,利用等比数列的通项公式及前n项和公式可求
(III)由(I)(II)可得, ,故考虑利用错位相减求数列的和
,故考虑利用错位相减求数列的和
点评:本题主要考查了利用基本量求解等差数列的通项公式及数列的和,及利用递推关系构造等比数列求解数列的通项公式,本题的难点在于(III)的错位相减求解数列的和
由a2=6,a5=18,
可得a1+d=6,a1+4d=18,
解得a1=2,d=4.
从而an=4n-2,Mn=2n2
(Ⅱ)由
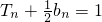 ,
,令n=1,则
 ,可得
,可得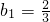 .
.当n≥2时,
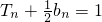 ,
, ,
,两式相减得
 .
.可得
 .
.所以数列{bn}是等比数列.
可得
 ,
, .…(8分)
.…(8分)(Ⅲ)由
 .
.则
 .
. .
.两式相减得
 .
.整理得

分析:(Ⅰ)设数列{an}的公差为d,由a2=6,a5=18,可求首项及公差,进而可求通项公式及前n项和
(Ⅱ)由
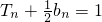 ,令n=1,可求
,令n=1,可求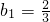 .当n≥2时,由
.当n≥2时,由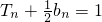 ,可得
,可得 ,两式相减得
,两式相减得 .即
.即 ,利用等比数列的通项公式及前n项和公式可求
,利用等比数列的通项公式及前n项和公式可求(III)由(I)(II)可得,
 ,故考虑利用错位相减求数列的和
,故考虑利用错位相减求数列的和点评:本题主要考查了利用基本量求解等差数列的通项公式及数列的和,及利用递推关系构造等比数列求解数列的通项公式,本题的难点在于(III)的错位相减求解数列的和

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目