题目内容
(2012•广东模拟)已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax-a-x+2(a>0,且a≠1),若g(2012)=a,则f(-2012)=( )
分析:由f(x)+g(x)=ax-a-x+2可得f(-x)+g(-x)=a-x-ax+2,结合f(-x)=-f(x),g(-x)=g(x)可求a,及f(x),代入可求
解答:解:∵f(x)+g(x)=ax-a-x+2①
∴f(-x)+g(-x)=a-x-ax+2
∵f(-x)=-f(x),g(-x)=g(x)
∴-f(x)+g(x)=a-x-ax+2②
联立①②可得,f(x)=ax-a-x,g(x)=2
∵g(2012)=a,
∴a=2
则f(-2012)=2-2012-22012
故选B
∴f(-x)+g(-x)=a-x-ax+2
∵f(-x)=-f(x),g(-x)=g(x)
∴-f(x)+g(x)=a-x-ax+2②
联立①②可得,f(x)=ax-a-x,g(x)=2
∵g(2012)=a,
∴a=2
则f(-2012)=2-2012-22012
故选B
点评:本题主要考查了奇偶函数的定义在函数解析式的求解中的应用,解题的关键是由g(x)确定a的值

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
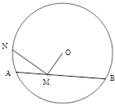 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=