题目内容
设各项均为正数的数列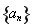 的前
的前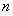 项和为
项和为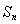 ,满足
,满足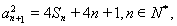 且
且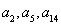 恰好是等比数列
恰好是等比数列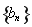 的前三项.
的前三项.
(Ⅰ)求数列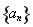 、
、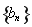 的通项公式;
的通项公式;
(Ⅱ)记数列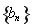 的前
的前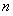 项和为
项和为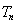 ,若对任意的
,若对任意的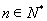 ,
, 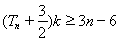 恒成立,求实数
恒成立,求实数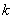 的取值范围.
的取值范围.
【答案】
(Ⅰ)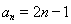 ,
,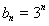 ;(Ⅱ)
;(Ⅱ) 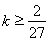
【解析】
试题分析:(Ⅰ)根据数列的通项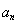 与数列前
与数列前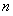 项和
项和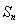 的关系,由
的关系,由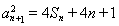 ,
,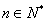 得
得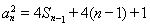 ;两式相减得数列
;两式相减得数列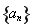 的递推公式
的递推公式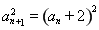 ,从而得出数列
,从而得出数列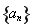 通项公式
通项公式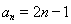 .由此可求
.由此可求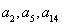 以确定等比数列
以确定等比数列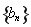 的首项和公比,进而得到数列
的首项和公比,进而得到数列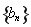 的通项公式.
的通项公式.
(Ⅱ)由(Ⅰ)的结果求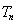 ,把
,把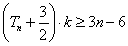 变形为,
变形为,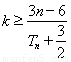 ,所以
,所以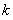 不小于
不小于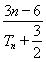 的最大值.
的最大值.
只需探究数列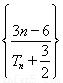 的单调性求其最大值即可.
的单调性求其最大值即可.
试题解析:(Ⅰ)当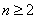 时,
时,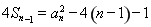 ,
,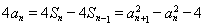
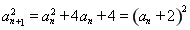 ,
,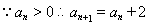 2分
2分
 当
当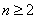 时,
时,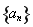 是公差
是公差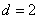 的等差数列.
的等差数列.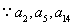 构成等比数列,
构成等比数列,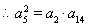 ,
,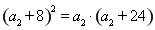 ,解得
,解得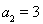 , 3分
, 3分
由条件可知,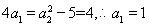 4分
4分
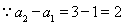

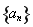 是首项
是首项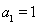 ,公差
,公差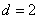 的等差数列.
的等差数列.
 数列
数列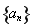 的通项公式为
的通项公式为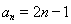 . 5分,
. 5分,
数列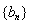 的通项公式为
的通项公式为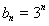 6分
6分
(Ⅱ) 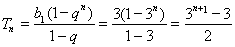 ,
, 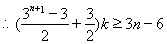 对
对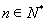 恒成立,
恒成立, 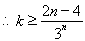 对
对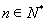 恒成立,----9分,
恒成立,----9分,
令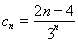 ,
,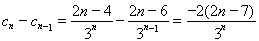 ,当
,当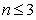 时,
时,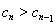 ,当
,当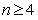 时,
时,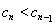
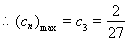 ,
,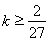 . 12分
. 12分
考点:1、等差数列;等比数列的通项公式和前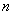 项和.2、参变量范围的求法.
项和.2、参变量范围的求法.

练习册系列答案
相关题目