Question

已知定义在R上的函数f(x)=asin(ωx)+bcos(ωx)(ω＞0)的周期为π，且f(x)≤f()=4．

（1）求函数f(x)的表达式；

（2）设不相等的实数x₁、x₂∈(0,π)，且f(x₁)=f(x₂)=-2，求x₁+x₂的值．

Answer 1

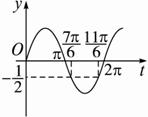
解:（1）f(x)=sin(ωx+φ)，由T=π,知ω=2,由f(x)≤4得, =4,①由f()=4知，asin +bcos=4,  ②  由①②解得a=2,b=2,∴f(x)的表达式为f(x)=2sin2x+2cos2x.(2)f(x)=4sin(2x+),由f(x₁)=f(x₂)=-2,令t=2x+,t₁=2x₁+,t₂=2x₂+，则有4sint₁=-2,4sint₂=-2,sint₁=sint₂=-,由x₁≠x₂?知t₁≠t₂，又x₁,x₂∈(0,π),∴t₁、t₂∈(,)，由y=sint的图象（下图）可知t₁+t₂=3π,即2(x₁+x₂)+ =3π,∴x₁+x₂=.