题目内容
 函数y=f(x)=Asin(ωx+θ),(A,ω,θ>0)在一个周期内的图象如图所示,D为图象的最高点,
函数y=f(x)=Asin(ωx+θ),(A,ω,θ>0)在一个周期内的图象如图所示,D为图象的最高点, 为图象与x轴的交点,且△BCD为正三角形.
为图象与x轴的交点,且△BCD为正三角形.
(Ⅰ)求y=f(x)的解析式;
(Ⅱ)若将y=f(x)的图象向右平移2个单位得到函数y=g(x),求y=g(x)的单调减区间.
解:(Ⅰ)由题意知BC= =
= +
+ =4,∴ω=
=4,∴ω= .
.
由五点法作图可得 +θ=0,∴θ=
+θ=0,∴θ= .
.
再由A= BC=2
BC=2 ,可得函数的解析式为
,可得函数的解析式为 .
.
(Ⅱ)由题意可得 ,
,
令 ,可得
,可得  ,k∈z.
,k∈z.
 ,即
,即  ,(k∈Z)
,(k∈Z)
故函数的减区间为 (k∈Z).
(k∈Z).
分析:(Ⅰ)由题意知BC= 求得ω,由五点法作图求得 θ,根据△BCD为正三角形求得振幅A,从而求得函数的解析式
求得ω,由五点法作图求得 θ,根据△BCD为正三角形求得振幅A,从而求得函数的解析式
(Ⅱ)函数y=Asin(ωx+∅)的图象变换规律,求得 ,令
,令 ,求得x的范围,即可得到函数的减区间.
,求得x的范围,即可得到函数的减区间.
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,函数y=Asin(ωx+∅)的图象变换规律,正弦函数的减区间,属于中档题.
 =
= +
+ =4,∴ω=
=4,∴ω= .
.由五点法作图可得
 +θ=0,∴θ=
+θ=0,∴θ= .
.再由A=
 BC=2
BC=2 ,可得函数的解析式为
,可得函数的解析式为 .
.(Ⅱ)由题意可得
 ,
,令
 ,可得
,可得  ,k∈z.
,k∈z. ,即
,即  ,(k∈Z)
,(k∈Z)故函数的减区间为
 (k∈Z).
(k∈Z).分析:(Ⅰ)由题意知BC=
 求得ω,由五点法作图求得 θ,根据△BCD为正三角形求得振幅A,从而求得函数的解析式
求得ω,由五点法作图求得 θ,根据△BCD为正三角形求得振幅A,从而求得函数的解析式(Ⅱ)函数y=Asin(ωx+∅)的图象变换规律,求得
 ,令
,令 ,求得x的范围,即可得到函数的减区间.
,求得x的范围,即可得到函数的减区间.点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,函数y=Asin(ωx+∅)的图象变换规律,正弦函数的减区间,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
②函数f(x)在[0,1]是减函数,在[1,2]是增函数; ③当1<a<2时,函数y=f(x)-a有4个零点; ④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最小值为0, 其中所有正确命题的个数是( ) |
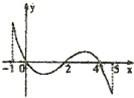 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示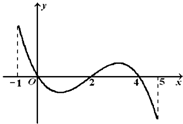

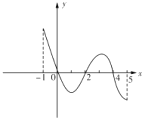 (2013•湖南模拟)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
(2013•湖南模拟)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.