题目内容
在△ABC中，cosB=
，b=6．
（1）当a=5时，求角A；
（2）当△ABC的面积为27时，求a+c的值．
，b=6．（1）当a=5时，求角A；
（2）当△ABC的面积为27时，求a+c的值．
解：（1）∵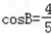 
＞0，∴B为锐角，且
，
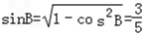由正弦定理得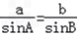
，可得
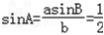
又∵a＜b，得角A＜B
∴A=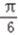
（舍
）
（2）∵△ABC的面积
，
，
∴
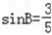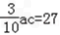，即ac=90．
由余弦定理得b2=a2+c2﹣2accosB
可得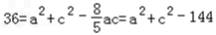
，即a2+c2=180．
∴（a+c）2=a2+c2+2ac=180+180=360，
所以，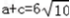
．
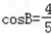＞0，∴B为锐角，且 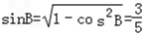，由正弦定理得
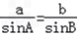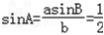
，可得 又∵a＜b，得角A＜B
∴A=
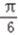（舍 ）（2）∵△ABC的面积
， ， ∴
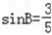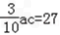，即ac=90．由余弦定理得b2=a2+c2﹣2accosB
可得
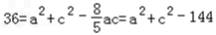，即a2+c2=180． ∴（a+c）2=a2+c2+2ac=180+180=360，
所以，
． 
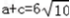练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
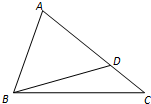如图，在△ABC中，cos∠ABC=