题目内容
定义区间 的长度均为
的长度均为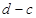 ,其中
,其中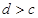 。已知实数
。已知实数 ,则满足
,则满足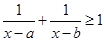 的
的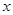 构成的区间的长度之和为 .
构成的区间的长度之和为 .
【答案】
2
【解析】
试题分析:原不等式等价于 。当
。当 或
或 时,原不等式等价于
时,原不等式等价于 。设
。设 ,则
,则 。设
。设 的两个根分别为
的两个根分别为 ,则满足
,则满足 的
的 构成的区间为
构成的区间为 ,区间的长度为
,区间的长度为 。当
。当 时,同理可得满足
时,同理可得满足 的
的 构成的区间为
构成的区间为 ,区间的长度为
,区间的长度为 。由韦达定理,
。由韦达定理, ,所以满足条件的
,所以满足条件的 构成的区间的长度之和为
构成的区间的长度之和为
考点:本题考查了一元二次方程的根
点评:此类问题通常转化为一元二次方程根的问题,难度比较大,关键是掌握一元二次方程中的韦达定理及根的分布

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 的长度均为
的长度均为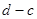 ,其中
,其中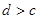 ,已知实数
,已知实数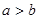 ,则满足
,则满足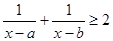 的x构成的区间长度之和为( )
的x构成的区间长度之和为( ) 的长度均为
的长度均为 已知实数
已知实数 ,则满足
,则满足 的
的 构成的区间的长度之和为
构成的区间的长度之和为 C.
C.
 D.
2
D.
2 的长度均为
的长度均为 已知实数
已知实数 ,则满足
,则满足 的
的 构成的区间的长度之和为
构成的区间的长度之和为 C.
C.
 D.
2
D.
2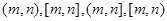 的长度均为
的长度均为 ,其中
,其中 ,已知关于
,已知关于 的不等式组
的不等式组 的解集构成的各区间长度和为4,则实数
的解集构成的各区间长度和为4,则实数 的取值范围是
▲ .
的取值范围是
▲ .