题目内容
已知a=(2，cosx)，b=(sin(x+
)，-2)，函数f(x)=a·b．(1)求函数f(x)的单调增区间；
(2)若f(x)=
，求cos(2x
)的值．
答案：f(x)=a·b=2sin(x+)-2cosx
=2sinxcos+2cosxsin-2cosx
=
sinx-cosx=2sin(x
)．
(1)由
+2kπ≤x
≤
+2kπ
得
+2kπ≤x≤
+2kπ
x∈[
+2kπ，
+2kπ]，k∈Z时，f(x)是增函数．
(2)由(1)知f(z)=2sin(x
)，f(x)=
即sin(x
)=
，
∴cos(2x
)=1-2sin2(x
)=
．
练习册系列答案
阅读快车系列答案
相关题目
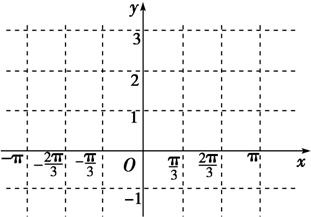已知a=2（cosωx，cosωx），b=（cosωx，
),且a∥b,则锐角θ等于（ ）
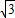sinωx）（其中0＜ω＜1），函数f（x）=a•b，若直线x=
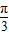是函数f（x）图象的一条对称轴，
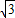sinωx）（其中0＜ω＜1），函数f（x）=a•b，若直线x=
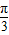是函数f（x）图象的一条对称轴，