题目内容
. (本小题满分12分）
如图,四棱锥P-ABCD的底面为等腰梯形,AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，已知AB=
，∠APB=∠ADB=60°
(Ⅰ)证明:平面PAC⊥平面PBD;
(Ⅱ)求PH与平面PAD所成的角的大小.
【答案】
（1）
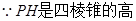
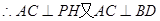
又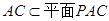
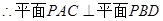
（2）过H作HE⊥AD于E，连结PE，则AD⊥平面PEH
又AD
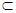平面PAD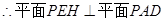 
过H作HG⊥PE于G，则HG⊥平面PAD，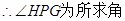
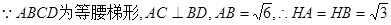
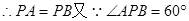∴△APB为等边三角形
，
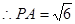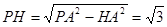
在Rt△ADH中,可得HD=1 ;在Rt△DEH中 ,可得HE=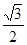
在Rt△PHE中 ,tan∠HPE=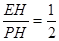
故PH与平面PAD所成角为arctan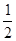
【解析】略
练习册系列答案
相关题目
的一元二次函数
（Ⅰ）设集合P={1，2， 3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为
和
，求函数
在区间[
上是增函数的概率；（Ⅱ）设点（
内的随机点，求函数
上是增函数的概率。
，且
。①求
的最大值及最小值；②求
的三视图如图所示，
,A1A=
,AB=
,AC=2,A1C1=1,
在线段
上且
=
.
⊥平面
；
的余弦值.