题目内容

已知数列{an}的相邻两项an，an+1是关于x的方程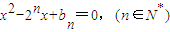的两根，且a1=1
（1）求证：数列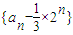是等比数列；
（2）求数列{an}的前n项和Sn；
（3）设函数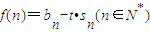，若f（n）＞0对任意的n∈N*都成立，求t的取值范围．
【答案】分析：（1）利用an，an+1是关于x的方程x2-2n•x+bn=0（n∈N*）的两实根，可得an+an+1=2n，整理变形可得数列是等比数列；
（2）确定数列的同学，分组求和，可得结论；
（3）关键bn=an•an+1，bn-tSn＞0，可得不等式，分类讨论，可求t的取值范围．
解答：（1）证明：∵an，an+1是关于x的方程x2-2n•x+bn=0（n∈N*）的两实根，
∴an+an+1=2n，∴
∴
∴数列是等比数列；
（2）解：∵a1=1，∴
∴Sn=a1+a2+…+an
=；
（3）解：∵bn=an•an+1，∴
∵bn-tSn＞0，∴
∴当n为奇数时，，∵n为奇数，∴t＜1；
当n为偶数时，，∴
∴t＜对任意正偶数n都成立，∴t＜
综上所述，t的取值范围为t＜1．
点评：本题主要考查等比关系的确定、数列的求和、不等式的解法、数列与函数的综合等基础知识，考查运算求解能力与转化思想．属于中档题．
练习册系列答案
相关题目
13、已知数列{an}的通项公式为an=（2n-1）•2n，我们用错位相减法求其前n项和Sn：由Sn=1×2+3×22+5×23+…（2n-1）•2n得2Sn=1×22+3×23+5×24+…（2n-1）•2n+1，两式项减得：-Sn=2+2×22+2×23+…+2×2n-（2n-1）•2n+1，求得Sn=（2n-3）•2n+1+6．类比推广以上方法，若数列{bn}的通项公式为bn=n2•2n，
则其前n项和Tn=
（n2-2n+3）•2n+1-6
．
已知数列{an}的通项为an=（2n-1）•2n，求其前n项和Sn时，我们用错位相减法，即
由Sn=1•2+3•22+5•23+…+（2n-1）•2n得2Sn=1•22+3•23+5•24+…+（2n-1）•2n+1
两式相减得-Sn=2+2•22+2•23+…+2•2n-（2n-1）•2n+1，
求出Sn=2-（2-2n）•2n+1．类比推广以上方法，若数列{bn}的通项为bn=n2•2n，则其前n项和Tn=
（n2-2n+3）•2n+1-6
（n2-2n+3）•2n+1-6
．
已知数列{an}的通项公式为an=（2n-1）•2n，我们用错位相减法求其前n项和Sn：由Sn=1×2+3×22+5×23+…（2n-1）•2n得2Sn=1×22+3×23+5×24+…（2n-1）•2n+1，两式项减得：-Sn=2+2×22+2×23+…+2×2n-（2n-1）•2n+1，求得Sn=（2n-3）•2n+1+6．类比推广以上方法，若数列{bn}的通项公式为bn=n2•2n，
则其前n项和Tn=______．
已知数列{an}的通项公式为an=（2n-1）•2n，我们用错位相减法求其前n项和Sn：由Sn=1×2+3×22+5×23+…（2n-1）•2n得2Sn=1×22+3×23+5×24+…（2n-1）•2n+1，两式项减得：-Sn=2+2×22+2×23+…+2×2n-（2n-1）•2n+1，求得Sn=（2n-3）•2n+1+6．类比推广以上方法，若数列{bn}的通项公式为bn=n2•2n，
则其前n项和Tn=    ．
已知数列{an}的通项公式为an=（2n-1）•2n，我们用错位相减法求其前n项和Sn：由Sn=1×2+3×22+5×23+…（2n-1）•2n得2Sn=1×22+3×23+5×24+…（2n-1）•2n+1，两式项减得：-Sn=2+2×22+2×23+…+2×2n-（2n-1）•2n+1，求得Sn=（2n-3）•2n+1+6．类比推广以上方法，若数列{bn}的通项公式为bn=n2•2n，
则其前n项和Tn=    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网