题目内容
已知函数f(x)=loga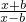 ,(a>0,b>0且a≠1),
,(a>0,b>0且a≠1),
(1)求f(x)的在定义域;
(2)讨论f(x)的单调性;(不要求证明)
(3)求f(x)的反函数.
解:(1)根据题意知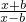 >0
>0
∴f(x)的在定义域是{x|x<-b,或x>b}
(2)当a>1时,f(x)在(-∝,-b)和(b,+∝)为单调递减函数;
当0<a<1时,f(x)在(-∝,-b)和(b,+∝)为单调递增函数
(3)∵y=loga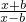
∴x=
∵y=loga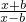 的值域为y≠0
的值域为y≠0
∴∴f-1(x)= (x≠0)
(x≠0)
分析:(1)根据真数大于0,求出f(x)的在定义域;
(2)根据符合函数的单调性,a分为两种情况讨论当a>1时,f(x)在(-∝,-b)和(b,+∝)为单调递减函数;当0<a<1时,f(x)在(-∝,-b)和(b,+∝)为单调递增
(3)根据指数与对数的关系求出x,然后求出原函数的值域就是反函数的定义域,即可求出反函数.
点评:本题考查了对数的定义域、函数单调性的判断以及反函数的求法,(3)问中要注意反函数的定义域,属于中档题.
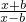 >0
>0∴f(x)的在定义域是{x|x<-b,或x>b}
(2)当a>1时,f(x)在(-∝,-b)和(b,+∝)为单调递减函数;
当0<a<1时,f(x)在(-∝,-b)和(b,+∝)为单调递增函数
(3)∵y=loga
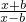
∴x=

∵y=loga
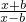 的值域为y≠0
的值域为y≠0∴∴f-1(x)=
 (x≠0)
(x≠0)分析:(1)根据真数大于0,求出f(x)的在定义域;
(2)根据符合函数的单调性,a分为两种情况讨论当a>1时,f(x)在(-∝,-b)和(b,+∝)为单调递减函数;当0<a<1时,f(x)在(-∝,-b)和(b,+∝)为单调递增
(3)根据指数与对数的关系求出x,然后求出原函数的值域就是反函数的定义域,即可求出反函数.
点评:本题考查了对数的定义域、函数单调性的判断以及反函数的求法,(3)问中要注意反函数的定义域,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目