题目内容
根据下列条件求椭圆或双曲线的标准方程.
(Ⅰ)已知椭圆的长轴长为6,一个焦点为(2,0),求该椭圆的标准方程.
(Ⅱ)已知双曲线过点P(
,
),渐近线方程为x±2y=0,且焦点在x轴上,求该双曲线的标准方程.
(Ⅰ)已知椭圆的长轴长为6,一个焦点为(2,0),求该椭圆的标准方程.
(Ⅱ)已知双曲线过点P(
| 5 |
| 1 |
| 2 |
(I)设椭圆的方程为
+
=1(a>b>0),则
∵椭圆的长轴长为6,一个焦点为(2,0),
∴2a=6,c=2,可得a=3,b2=
=5
因此,椭圆的方程为
+
=1;
(II)∵双曲线渐近线方程为x±2y=0,
∴设双曲线方程为x2-4y2=λ(λ≠0)
∵点P(
,
)在双曲线上,∴(
)2-4×(
)2=λ,可得λ=4
因此,双曲线方程为x2-4y2=4,化成标准方程为
-y2=1.
即所求双曲线方程为
-y2=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的长轴长为6,一个焦点为(2,0),
∴2a=6,c=2,可得a=3,b2=
| a2-c2 |
因此,椭圆的方程为
| x2 |
| 9 |
| y2 |
| 5 |
(II)∵双曲线渐近线方程为x±2y=0,
∴设双曲线方程为x2-4y2=λ(λ≠0)
∵点P(
| 5 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
因此,双曲线方程为x2-4y2=4,化成标准方程为
| x2 |
| 4 |
即所求双曲线方程为
| x2 |
| 4 |

练习册系列答案
相关题目
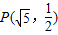 ,渐近线方程为x±2y=0,且焦点在x轴上,求该双曲线的标准方程.
,渐近线方程为x±2y=0,且焦点在x轴上,求该双曲线的标准方程.