题目内容
函数 的
的
- A.最大值是

- B.最小值是

- C.最大值是
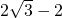
- D.最小值是
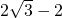
D
分析:先把 等价转化为f(x)=
等价转化为f(x)= ,再由x>0,利用均值不等式知f(x)≥
,再由x>0,利用均值不等式知f(x)≥ ,由此能求出其最大值.
,由此能求出其最大值.
解答:∵x>0,
∴
=
≥
=2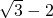 .
.
当且仅当 ,即x=
,即x= 时,
时,
函数 取最小值2
取最小值2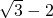 .
.
故选D.
点评:本题考查均值不等式的应用,是基础题.解题时要认真审题,仔细解答.易错点是忽视均值不等式的应用条件:一正、二定、三相等.
分析:先把
 等价转化为f(x)=
等价转化为f(x)= ,再由x>0,利用均值不等式知f(x)≥
,再由x>0,利用均值不等式知f(x)≥ ,由此能求出其最大值.
,由此能求出其最大值.解答:∵x>0,
∴

=

≥

=2
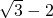 .
.当且仅当
 ,即x=
,即x= 时,
时,函数
 取最小值2
取最小值2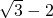 .
.故选D.
点评:本题考查均值不等式的应用,是基础题.解题时要认真审题,仔细解答.易错点是忽视均值不等式的应用条件:一正、二定、三相等.

练习册系列答案
相关题目