题目内容
 在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1中点.
在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1中点.(1)求证:平面B1FC1∥平面ADE;
(2)试在棱DC上求一点M,使D1M⊥平面ADE
(3)求二面角A1-DE-A的余弦值.
分析:(1)证明四边形DFB1E为平行四边形,再利用AD∥B1C1,这样,面平面B1FC内有2条相交线B1C1和B1F平行于另一个平面.
(2)取DC中点M,证明D1M⊥B1C1,D1M⊥FC1,从而D1M⊥平面B1FC1,再根据平面B1FC1∥平面ADE,证得D1M⊥平面ADE.
(3)以D为原点,端点在D的三条棱为坐标轴建立坐标系,写出要用的点的坐标,得到
=(2,0,2),
=(2,2,1),设出平面A1DE的法向量,根据两个向量之间的垂直关系求出平面的法向量,另一个平面的法向量是存在于图形中,根据两个向量的夹角的余弦值做出结果.
(2)取DC中点M,证明D1M⊥B1C1,D1M⊥FC1,从而D1M⊥平面B1FC1,再根据平面B1FC1∥平面ADE,证得D1M⊥平面ADE.
(3)以D为原点,端点在D的三条棱为坐标轴建立坐标系,写出要用的点的坐标,得到
| DA1 |
| DE |
解答: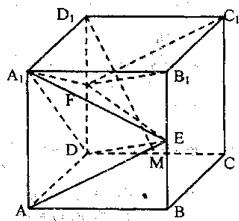 解:(1)证明:∵E、F分别为正方体ABCD-A1B1C1D1棱BB1和DD1中点.
解:(1)证明:∵E、F分别为正方体ABCD-A1B1C1D1棱BB1和DD1中点.
∴DF∥B1E且DF=B1E
∴四边形DFB1E为平行四边形,
即FB1∥DE,
由∵AD∥B1C1(2分)
又AD∩DE=D,B1C1∩B1F=B1
∴平面B1FC∥平面ADE.(4分)
(2)证明:取DC中点M,连接D1M,
由正方体性质可知,D1M⊥B1C1,
且△DD1M≌△C1D1F (5分)所以∠D1C1F=∠DD1M,
又∠D1C1F+∠D1FC1=900
所以∠D1D1M+∠D1FC1=900
所以D1M⊥FC1(6分
又FC1∩B1C1=C1
∴D1M⊥平面B1FC1
又由(1)知平面B1FC1∥平面ADE.
所以D1M⊥平面ADE.(8分)
(3)以D为原点,端点在D的三条棱为坐标轴建立坐标系,写出要用的点的坐标,
得到
=(2,0,2),
=(2,2,1),
设平面A1DE的法向量是
=(p,q,r),
则有2p+2r=0,
2p+2q+r=0,
令p=1,得r=-1,q=-
,
∴
=(1,-
,-1)
由(2)知平面ADE的法向量是(0,1,-2)
∴二面角的余弦值是
 解:(1)证明:∵E、F分别为正方体ABCD-A1B1C1D1棱BB1和DD1中点.
解:(1)证明:∵E、F分别为正方体ABCD-A1B1C1D1棱BB1和DD1中点.∴DF∥B1E且DF=B1E
∴四边形DFB1E为平行四边形,
即FB1∥DE,
由∵AD∥B1C1(2分)
又AD∩DE=D,B1C1∩B1F=B1
∴平面B1FC∥平面ADE.(4分)
(2)证明:取DC中点M,连接D1M,
由正方体性质可知,D1M⊥B1C1,
且△DD1M≌△C1D1F (5分)所以∠D1C1F=∠DD1M,
又∠D1C1F+∠D1FC1=900
所以∠D1D1M+∠D1FC1=900
所以D1M⊥FC1(6分
又FC1∩B1C1=C1
∴D1M⊥平面B1FC1
又由(1)知平面B1FC1∥平面ADE.
所以D1M⊥平面ADE.(8分)
(3)以D为原点,端点在D的三条棱为坐标轴建立坐标系,写出要用的点的坐标,
得到
| DA1 |
| DE |
设平面A1DE的法向量是
| m |
则有2p+2r=0,
2p+2q+r=0,
令p=1,得r=-1,q=-
| 1 |
| 2 |
∴
| m |
| 1 |
| 2 |
由(2)知平面ADE的法向量是(0,1,-2)
∴二面角的余弦值是
| ||
| 5 |
点评:本题考查的知识点是用空间向量求平面与平面的夹角,向量语言表述线面的垂直、平行关系,其中建立空间坐标系,将空间线面的夹角及垂直、平行问题转化为向量问题是解答此类问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.  如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )
如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )