题目内容
设函数y=f(x)(x∈R且x≠0)对任意非零实数x1,x2恒有f(x1x2)=f(x1)+f(x2),且对任意x>1,
f(x)<0。
(Ⅰ)求f(-1)及f(1)的值;
(Ⅱ)判断函数f(x)的奇偶性;
(Ⅲ)求方程 的解。
的解。
f(x)<0。
(Ⅰ)求f(-1)及f(1)的值;
(Ⅱ)判断函数f(x)的奇偶性;
(Ⅲ)求方程
 的解。
的解。 解:(Ⅰ)对任意非零实数 恒有
恒有 ,
,
∴令 ,代入可得
,代入可得 ,
,
又令 ,代入并利用
,代入并利用 ,可得
,可得 。
。
(Ⅱ)取 ,代入,得
,代入,得 ,
,
又函数的定义域为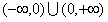 ,
,
∴函数 是偶函数。
是偶函数。
(Ⅲ)函数f(x)在(0,+∞)上为单调递增函数,证明如下:
任取 且
且 ,则
,则 ,由题设有
,由题设有 ,
,
∴ ,
,
∴ ,即函数f(x)在
,即函数f(x)在 上为单调递增函数;
上为单调递增函数;
由(Ⅱ)函数f(x)是偶函数,
∴函数f(x)在 上为单调递减函数;
上为单调递减函数;
∴ ,
,
解得: 或x=2,
或x=2,
∴方程 的解集为
的解集为 。
。
 恒有
恒有 ,
,∴令
 ,代入可得
,代入可得 ,
,又令
 ,代入并利用
,代入并利用 ,可得
,可得 。
。(Ⅱ)取
 ,代入,得
,代入,得 ,
,又函数的定义域为
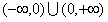 ,
,∴函数
 是偶函数。
是偶函数。(Ⅲ)函数f(x)在(0,+∞)上为单调递增函数,证明如下:
任取
 且
且 ,则
,则 ,由题设有
,由题设有 ,
,∴
 ,
,∴
 ,即函数f(x)在
,即函数f(x)在 上为单调递增函数;
上为单调递增函数;由(Ⅱ)函数f(x)是偶函数,
∴函数f(x)在
 上为单调递减函数;
上为单调递减函数;∴
 ,
,解得:
 或x=2,
或x=2,∴方程
 的解集为
的解集为 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目