题目内容
已知点![]() 是直角坐标平面内的动点,点
是直角坐标平面内的动点,点![]() 到直线
到直线![]() (
(![]() 是正常数)的距离为
是正常数)的距离为![]() ,到点
,到点![]() 的距离为
的距离为![]() ,且
,且![]() 1.
1.
(1)求动点P所在曲线C的方程;
(2)直线![]() 过点F且与曲线C交于不同两点A、B,分别过A、B点作直线
过点F且与曲线C交于不同两点A、B,分别过A、B点作直线![]() 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为![]() ,求证
,求证![]() =
=![]() ;
;
(3)记![]() ,
,![]() ,
,![]() (A、B、
(A、B、![]() 是(2)中的点),
是(2)中的点),![]() ,求
,求![]() 的值.
的值.
 解 (1) 设动点为
解 (1) 设动点为![]() , 1分
, 1分
依据题意,有
![]() ,化简得
,化简得![]() . 4分
. 4分
因此,动点P所在曲线C的方程是:![]() . ……………………6分
. ……………………6分
由题意可知,当过点F的直线![]() 的斜率为0时,不合题意,
的斜率为0时,不合题意,
故可设直线![]() :
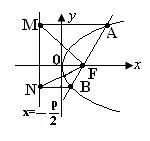
:![]() ,如图所示. 8分
,如图所示. 8分
联立方程组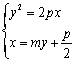 ,可化为
,可化为![]() ,
,
则点![]() 的坐标满足
的坐标满足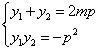 . 10分
. 10分
又![]() 、
、![]() ,可得点
,可得点![]() 、
、![]() .
.
于是,![]() ,
,![]() ,
,
因此![]() . 12分
. 12分
(3)依据(2)可算出![]() ,
,![]() ,
,
则 ![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() . 16分
. 16分
所以,![]() 即为所求. 18分
即为所求. 18分

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 是直角坐标平面内的动点,点
是直角坐标平面内的动点,点 (
(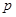 是正常数)的距离为
是正常数)的距离为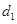 ,到点
,到点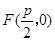 的距离为
的距离为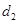 ,且
,且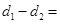 1.
1.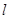 过点F且与曲线C交于不同两点A、B,分别过A、B点作直线
过点F且与曲线C交于不同两点A、B,分别过A、B点作直线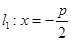 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为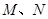 ,求证
,求证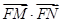 =
= ;
;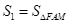 ,
, ,
,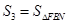
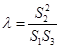 ,求
,求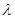 的值.
的值. 是直角坐标平面内的动点,点
是直角坐标平面内的动点,点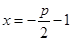 (
(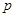 是正常数)的距离为
是正常数)的距离为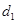 ,到点
,到点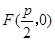 的距离为
的距离为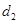 ,且
,且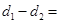 1.
1.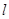 过点F且与曲线C交于不同两点A、B,分别过A、B点作直线
过点F且与曲线C交于不同两点A、B,分别过A、B点作直线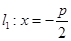 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为 ,求证
,求证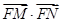 =
= ;
;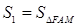 ,
,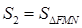 ,
,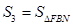 (A、B、
(A、B、 是(2)中的点),
是(2)中的点),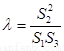 ,求
,求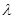 的值.
的值.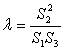 ,求
,求