题目内容
已知三角形的三边长分别为4、6、8，则此三角形为（ ）
分析：不妨设a=4，b=6，c=8，可得C是最大角．根据余弦定理，算出cosC是负数，从而得到角C是钝角，由此得到此三角形为
钝角三角形．
钝角三角形．
解答：解：三角形的三边长分别为4、6、8，
不妨设A、B、C所对的边分别为a、b、c，且a=4，b=6，c=8
∵c=8是最大边，∴角C是最大角
根据余弦定理，得cosC=
=
＜0
∵C∈（0，π）
∴角C是钝角，可得△ABC是钝角三角形
故选：D
不妨设A、B、C所对的边分别为a、b、c，且a=4，b=6，c=8
∵c=8是最大边，∴角C是最大角
根据余弦定理，得cosC=
| a2+b2-c2 |
| 2ab |
| 16+36-64 |
| 2×4×6 |
∵C∈（0，π）
∴角C是钝角，可得△ABC是钝角三角形
故选：D
点评：本题给出三角形的三条边长，判断三角形的形状，着重考查了用余弦定理解三角形和余弦函数的取值等知识，属于基础题．
练习册系列答案
相关题目
，
且m＞0，则这个三角形的最大角为已知三角形的三边长分别是
2m＋3，
，
且m＞0，则这个三角形的最大角为
[
]|
A ．150° |
B ．135° |
|
C ．120° |
D ．90° |
,则此三角形中的最大角是( )
的三边长
,满足
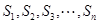均为正整数,且
,且
,求满足不等式
的所有
的值;
满足
,证明数列
中的任意连续三项为边长均可以构成直角三角形,且
是正整数.
，它的面积可用海伦—秦九韶公式计算。
，其中