题目内容
15.已知点P为y轴上的动点,点M为x轴上的动点.点F(1,0)为定点,且满足$\overrightarrow{PN}$+$\frac{1}{2}$$\overrightarrow{NM}$=$\overrightarrow{0}$,$\overrightarrow{PM}$•$\overrightarrow{PF}$=0.(Ⅰ)求动点N的轨迹E的方程.
(Ⅱ)A,B是E上的两个动点,l为AB的中垂线,求当l的斜率为2时,l在y轴上的截距m的范围.
分析 (Ⅰ)设出N点的坐标,由已知条件$\overrightarrow{PN}$可知P为MN的中点,由题意设出P和M的坐标,求出$\overrightarrow{PM}$和$\overrightarrow{PF}$的坐标,代入$\overrightarrow{PM}$•$\overrightarrow{PF}$可求动点N的轨迹E的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),l方程为y=2x+m,则AB的方程为:$y=-\frac{1}{2}x+b$,直线与圆锥曲线联立求得中点坐标,继而求出答案.
解答 解::(Ⅰ)设动点N的坐标为(x,y),P(0,b)M(a,0)则$\overrightarrow{PN}=(x,y-b),\overrightarrow{NM}=(a-x,-y)$,
$\overrightarrow{PM}=(a,-b),\overrightarrow{PF}=(1,-b)$,由$\overrightarrow{PN}+\frac{1}{2}\overrightarrow{NM}=\overrightarrow{0}$,$\overrightarrow{PM}•\overrightarrow{PF}=0$,可得$\left\{\begin{array}{l}{x+\frac{1}{2}(a-x)=0}\\{y-b-\frac{1}{2}y=0}\\{a+{b}^{2}=0}\end{array}\right.$,
∴y2=4x;
(Ⅱ)设A(x1,y1),B(x2,y2),l方程为y=2x+m,则AB的方程为:$y=-\frac{1}{2}x+b$,
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=-\frac{1}{2}x+b}\end{array}\right.$可得:x2-4(b+4)x+4b2=0,△=16(b+4)2-16b2>0,∴b>-2,
x1+x2=4(b+4),∴AB的中点坐标为(2b+8,-4),-4=4b+16+m
∴m=-4b-20,故:m∈(-∞,-12).
点评 本题考查了轨迹方程的求法,考查了平面向量数量积的运算,考查了直线与圆锥曲线的关系,直线与圆锥曲线的关系问题是考查的中点,常和弦长问题、存在性问题结合考查,解答时往往采用“设而不求”的解题方法,借助于一元二次方程的根与系数关系解题,该种类型的问题计算量较大,要求学生有较强的运算能力,是难题.

| A. | h(x1)<0,h(x2)<0 | B. | h(x1)>0,h(x2)>0 | C. | h(x1)>0,h(x2)<0 | D. | h(x1)<0,h(x2)>0 |
| A. | a=1 | B. | a=-1 | C. | a=2 | D. | a=1 |
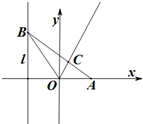 如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.
如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.