题目内容
已知△ABC顶点B(-
,0),C(
,0)(a>0),点A满足sinC-sinB=
sinA,则顶点A的轨迹方程是( )
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
分析:利用正弦定理可得A是以B,C为焦点的双曲线的右支(除去三点共线情况),根据△ABC顶点B(-
,0),C(
,0)(a>0),可得顶点A的轨迹方程.
| a |
| 2 |
| a |
| 2 |
解答:解:∵点A满足sinC-sinB=
sinA,∴由正弦定理可得AB-AC=
BC,
∴A是以B,C为焦点的双曲线的右支(除去三点共线情况),
∵△ABC顶点B(-
,0),C(
,0)(a>0),
∴顶点A的轨迹方程是
x2-
y2=1(x>
),
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
∴A是以B,C为焦点的双曲线的右支(除去三点共线情况),
∵△ABC顶点B(-
| a |
| 2 |
| a |
| 2 |
∴顶点A的轨迹方程是
| 16 |
| a2 |
| 16 |
| 3a2 |
| a |
| 4 |
故选C.
点评:本题考查双曲线的定义,考查双曲线的标准方程,考查学生的转化能力,属于中档题.

练习册系列答案
相关题目
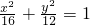 的两个焦点,顶点A在该椭圆上,则
的两个焦点,顶点A在该椭圆上,则 =________.
=________. 的两个焦点,顶点A在该椭圆上,则
的两个焦点,顶点A在该椭圆上,则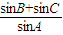 = .
= .