题目内容
已知:函数![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求![]() 在
在![]() 内的值域;
内的值域;
(2)若![]() 的解集为
的解集为![]() ,求
,求![]() 的取值范围.
的取值范围.
解析:由题意可知![]() 的两根分别为
的两根分别为![]() ,且
,且![]() ,
,
则由韦达定理可得: .
.
故![]() ……………………4分
……………………4分
(1)![]() 在
在![]() 内单调递减,故
内单调递减,故![]()
故![]() 在
在![]() 内的值域为
内的值域为![]() . ……………………8分
. ……………………8分
(2)![]() ,则要使
,则要使![]() 的解集为R,只需要方程
的解集为R,只需要方程 ![]() 的判别式
的判别式![]() ,即
,即![]() ,解得
,解得![]() .
.
∴当![]() 时,
时,![]() 的解集为
的解集为![]() . ……………………12分
. ……………………12分

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 为奇函数,当
为奇函数,当 时,
时, ,则
,则 ______.
______. ,当
,当 时
时 ,则
,则 =
.
=
. ,当
,当 时
时 ,则
,则 = ( )
= ( ) ,记函数
,记函数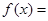

 时,求函数
时,求函数 的值域;
的值域; 时的最大值与最小值.
时的最大值与最小值. 为奇函数,当
为奇函数,当 时
时 ,则当
,则当 时,
时,
 ( )
( ) B
B
 C
C
 D
D
